国电 | ADC采样与频谱分析的技巧

题目

本以为国电选信号失真度测量装置（A 题）题（几乎和之前的校赛一模一样），难度就会大大下降，结果还是要和所有人一起从零开始熟悉MSP430系列，最后测评还出问题了，寄。

题目这里就不贴了，在校赛的基础上改为直接测量外部信号发生器产生的波形，限定使用MSP430系列，电压范围30mV ~ 600mV，基频固定1kHz，失真度误差在5%以内，发挥部分大概就是手机显示波形和测量结果，更宽的电压范围和更小的误差范围以及1kHz ~100kHz基频范围。

思路

看到这里我大概知道只要把输入信号稍微放大，ADC采样后用FFT分析即可，至于变基频无非就是写算法找频谱峰值，宽电压范围有点麻烦，需要做变增益控制，不过这个可以放着，而手机显示外接个蓝牙串口也可以完成。

大部分的麻烦在ADC采样，我们用的MSP430P401R看上去ADC也只有最大1Mbps，按照手册典型的时钟是25Mhz，完成一次完整ADC至少需要22个时钟周期，但是实际上我们用定时器触发采样，略高于1Mhz启动ADC都不行

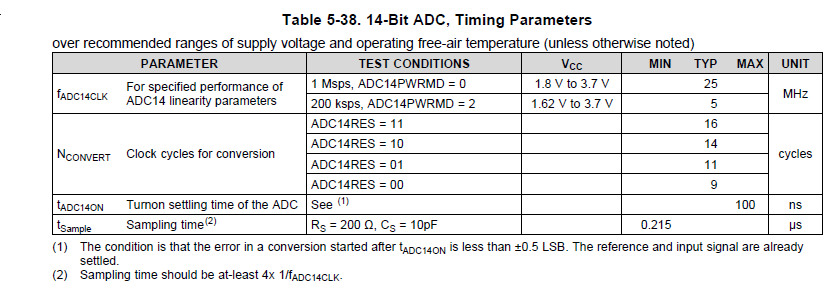
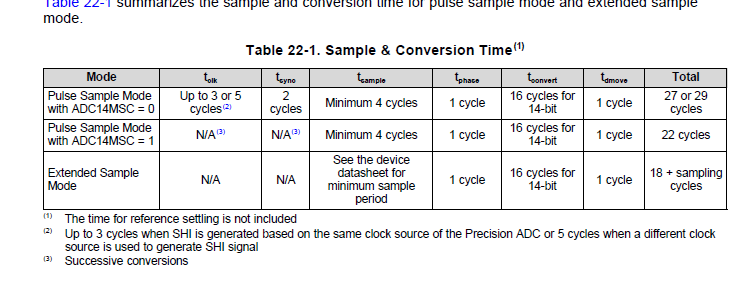
第二个问题在于高速ADC采样储存结果需要DMA，但是从手册和实际结果看，配置一次DMA最大只能传输1024个结果，相当于一次连续采样只能最多分析1024个结果，所以在比赛的时候我认为在这方面发挥的余地非常小。

ADC技巧

实际上在比赛之后我才发现在这方面的操作实在太多了，首先需要解释一下目前主流片内SAR（逐次逼近型） ADC的原理。

完成ADC至少需要经过采样保持，转换两个步骤，其中采样保持相当于将模拟电压保存下来，确保在后续转换中不会改变，而转换则是将采样值转换为数字量，而SAR的原理是，按位二分比较电压值输出下一位的值，例如在0 - 3.3V的电压范围转换1.3V，首先1.3V < 3.3V/2那么最高位为0，而1.3V > 3.3V/2因此次高位为1，以此类推直到转换至最低位。

回到题目，题目有一个压得非常极限的指标就是100kHz，由于我们需要采到5次谐波即500kHz。根据奈奎斯特采样准则，1Mbps的采样率在500kHz处可能会发生混叠，具体取决于采样点相对于波形的相位。那么如何解决采样率不够的问题呢？

通常情况下，ADC完成采样保持的时间远远小于完成转换的时间，这也就意味着如果我们有不止一个ADC转换器，我们可以通过流水线的方式提升ADC的采样速度。但是显然我们的硬件上就没有多的转换器，所以这个想法是行不通的。赛后上网搜了一圈，关于这个问题解决的方案其实不止一种：

大力出奇迹型：硬件够强足矣

我是真的没想到原来是有2Mbps ADC的MSP430，它的型号是MSP432E401Y

励志型：我们来多几次

实际上我们忽略了题目中隐含的一个信息，我们要做的是周期信号的分析，而不是杂乱无章的无周期。也就是说模拟信号输入会重复若干次，这个时候如果我们能够在一个相位触发一次连续固定采样率的ADC，下一次在这个相位延迟确定的时间后再触发一次，就有可能获得ADC采样点中间的采样值，这样相当于提高采样率。即使这个延迟不确定也有机会通过算法恢复延迟的时间长度。

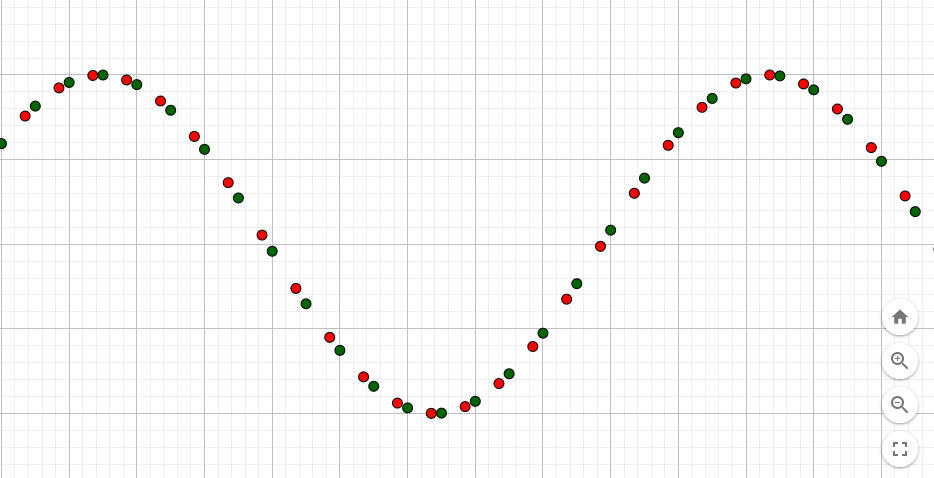
这种办法的专业术语叫做等效采样 或者等效时间采样，主要应用于数字示波器。这个办法也是复盘中我认为最接近发挥部分的预期解（说不定出题人想让我们做个示波器）

摆烂型：混叠什么的无所谓

又是题目隐含的信息，我们输入信号是由五个频点的信号叠加而成的，也就是说对这道题来讲有用的频谱也就是那5个尖峰而已，我们并没有要求分析整个连续的频谱。于是我们可以通过经过设计的采样率，让混叠的频谱不在这五个尖峰上就可以了。

例如以100kHz+5次谐波为例，上频谱图是采样率1MHz而下频谱图为900kHz，可以看到1Mhz采样率存在两个尖峰的混叠，而900kHz的可以让500kHz频谱展现出来。

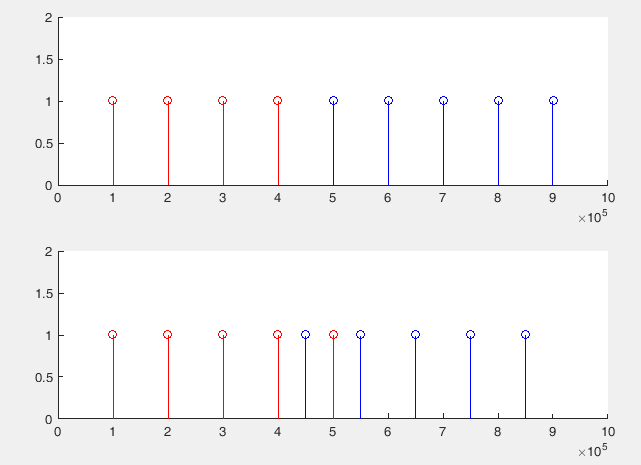
所以实际上为了还原频谱除了提高采样率避免混叠外，还可以刻意降低采样率以让高频进入可以采样的范围内。

算法

除了硬件部分外软件部分的算法也比较重要，在比赛时我们还写了一个Python脚本验证算法以及误差

import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft

V_REF = 3.3
V_REF_MID_ADC = int((2**14)/2)

F_BASE = 100e+3
F_SAMPLE = 0.95e+6
#F_SAMPLE = F_BASE*9.5
#SAMPLE_POINT_NUM = int(F_SAMPLE/F_BASE)
SAMPLE_POINT_NUM = int(1000)

# HARM1 = 0.3
# HARM2 = 0.02
# HARM3 = 0.05
# HARM4 = 0.01
# HARM5 = 0.04
HARM1 = 0.02
HARM2 = 0
HARM3 = 0
HARM4 = 0
HARM5 = 0.002


def goertzel_mag(y,length,f):
	q0 = 0.0
	q1 = 0.0
	q2 = 0.0
	Wn = 0.0
	#k = float(length * f) 
	omega = (2.0 * np.pi * f) / F_SAMPLE
	sine = np.sin(omega)
	coeff = 2 * np.cos(omega)
	
	#print(coeff)
	for i in range(length):
		Wn = 0.5 - 0.5*np.cos(2.0 * np.pi*i/(length - 1));
		#Wn=1
		q0 = coeff * q1 - q2 + y[i]*Wn
		q2 = q1
		q1 = q0
	magnitude2 = q1*q1 + q2*q2 - q1*q2*coeff
	#real = (q1 - q2 * cosine)
	#imag = q2 * sine
	#magnitude2 = real*real + imag*imag
	return np.sqrt(magnitude2)/(length/2)
    

t = np.linspace(0,SAMPLE_POINT_NUM-1,SAMPLE_POINT_NUM)
omega = 2*np.pi*F_BASE/F_SAMPLE

analog_y = HARM1 * np.sin(omega*t) +HARM2 * np.sin(2*omega*t) +HARM3 * np.sin(3*omega*t) + HARM4 * np.sin(4*omega*t) + HARM5 * np.sin(5*omega*t)

adc_y = ((analog_y / V_REF)*(2**14)).astype(int) + V_REF_MID_ADC

adc_y = adc_y.clip(min=0,max=(2**14)-1)

real_THD = np.sqrt(HARM2*HARM2+HARM3*HARM3+HARM4*HARM4+HARM5*HARM5)/HARM1

print("real_THD = {:.8%}".format(real_THD))

voltage = adc_y.astype(float)/(2**14)*V_REF

f_cal=F_BASE
goertzel_pnum = SAMPLE_POINT_NUM

harm1_est = goertzel_mag(voltage,goertzel_pnum,f_cal)
harm2_est = goertzel_mag(voltage,goertzel_pnum,f_cal*2)
harm3_est = goertzel_mag(voltage,goertzel_pnum,f_cal*3)
harm4_est = goertzel_mag(voltage,goertzel_pnum,f_cal*4)
harm5_est = goertzel_mag(voltage,goertzel_pnum,f_cal*5)

print("%f,%f,%f,%f,%f" % (harm1_est,harm2_est,harm3_est,harm4_est,harm5_est))

est_THD = np.sqrt(harm2_est*harm2_est+harm3_est*harm3_est+harm4_est*harm4_est+harm5_est*harm5_est)/harm1_est

print("est_THD = {:.8%}".format(est_THD))

经过上面的仿真之后至少说明了：

• Goertzel与FFT算法计算出的结果并无区别
• 量化误差等微小噪声对输出影响不大，可以符合题目要求
• 当采样波形的时间恰好等于波形本身的周期整数倍时，恰好无频谱泄露。当然实际上在不同频率要做到这一点也十分困难，为了解决非周期截断的问题后面需要增加窗函数，结果上看来Hamming窗效果最好

总结

上面总结的两种方法其实都是属于欠采样技术，如果是现实中采连续频谱的话可能还要加一个抗混叠滤波器，不过针对国电题目来讲不需要罢了。虽然国电并没有拿到名次，但是也让我恶补了上面ADC的常识，不亏。