坐标旋转数字计算CORDIC的实现

CORDIC（Coordinate Rotation Digital Computer）算法即坐标旋转数字计算，这个算法的神奇之处在于它可以借助加减法、移位以及查表完成常见的超越函数（三角函数，反三角函数，对数，开根号）的计算，而不用多项式展开或者浮点数的计算。

原理

所谓坐标旋转可以理解为在例如直角坐标系下的通过旋转矢量完成求解，对于一个坐标(x,y) 可以由初始(x_0,y_0)通过旋转矩阵得来，即

以计算正弦和余弦为例，CORDIC算法是预先求出(1/2)^n的反正切制成一个表，当我们输入一个预期角度时，通过比较当前角度与预期角度的大小确定旋转的方向d(仅代表正负符号)，然后计算

巧妙的一点是，(1/2)^n恰好可以用右移来完成，而cos(theta)则是作为一个缩放因子，在迭代次数固定时也可以累乘预先计算。

这个迭代每次都会查表并且把反正切对应的角度加入当前角度，直到指定的迭代次数。这时计算出的角度应该非常接近对应角度，而旋转出的x_(n+1),y_(n+1)则应该是分别对应经过缩放的正弦值和余弦值。

从另外一个角度看，这可以说是二分法查找正弦值和余弦值，但是通过旋转的计算降低了表的大小，同时可以看到输出精度非常容易控制，在每次迭代后结果都会增加1bit。

这个算法当然还可以计算其他函数。通过比较角度确定旋转方向被称作Rotation mode，还有另外一种方法叫Vectoring mode，顾名思义就是比较矢量(x或y其中一个)确定旋转方向，这种办法可以求反正切函数。

而旋转的坐标系也可以变为线性坐标系（乘法计算），双曲坐标系（计算指数对数），后者与上述直角坐标系的区别仅仅在于把正切函数换成了双曲正切。也即相当于

不过在双曲坐标系下，矢量长度变为

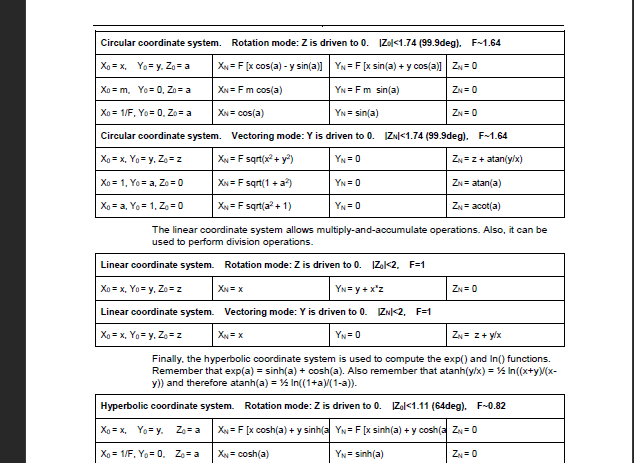
其他具体的方法可以查这份文档里的表格

实现

这种算法被广泛用于FPGA实现求超越函数，当然在没有浮点的STM32中这种算法也是相当有价值的。

除了刚才的文档外，ST官方也在这里给出了详细的定点计算实现代码以及精度测试，包括表和参数的生成。

不论哪种模式本质上都是旋转对应坐标系下的矢量，而其长度不变。一般想计算几种模式的组合输出值只需要考虑末态即结束条件下的旋转结果即可。例如Circular coordinate system. Vectoring mode Y -> 0则输出结果则是将矢量旋转至X轴上，X的大小即为矢量长度sqrt(x^2 + y^2)，而转过的角度差即为矢量的正切值即atan(y/x)

其中两种模式和三种坐标系的组合的输出值ST文档里的表格基本都给出了，不过有一种特殊的Vectoring mode是迫使Y等于输入值a，这种办法可以计算asin和acos，详细配置如下

Circular coordinate system. Vectoring mode: Y is driven to a.
输入X0 = x, Y0 = y, Z0 = z
输出XN = F*sqrt(x^2+y^2-a^2) ,YN = a ZN = z + arcsin(a/sqrt(x^2+y^2))

Circular coordinate system. Vectoring mode: X is driven to a.
输入X0 = x, Y0 = y, Z0 = z
输出XN = a ,YN = F*sqrt(x^2+y^2-a^2), ZN = z + arccos(a/sqrt(x^2+y^2))

使用的时候还需要注意收敛角度，即输入值需要在一定范围内迭代才会收敛，这一点在文档里也给出了

ST代码唯一的问题是在双曲坐标系下程序生成的表的长度不对，跳过了第一个（原因是反双曲在0时应该是无限大），把这里n=0时的输出改为0不旋转角度即可

当然民间还有浮点版本的，这里不再赘述

性能

Benchmark用的代码

没开任何优化的情况下，似乎在没有浮点加速的STM32F103上这个算法跑起来没有math.h里面的一次sinf和cosf快

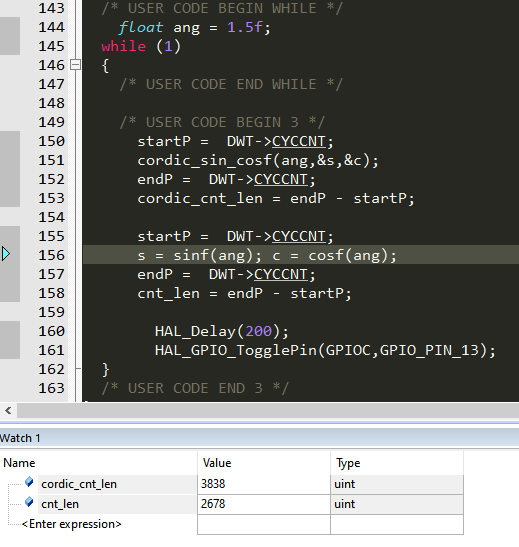
用DWT 72Mhz时钟计时换算过来是CORDIC算一次正弦+余弦耗时53.3us，而math库里面的单精度浮点sinf和cosf加起来耗时37.1us

然而开满优化之后(-O3 -Otime)，CORIDC速度直接起飞，耗时低至13.3us

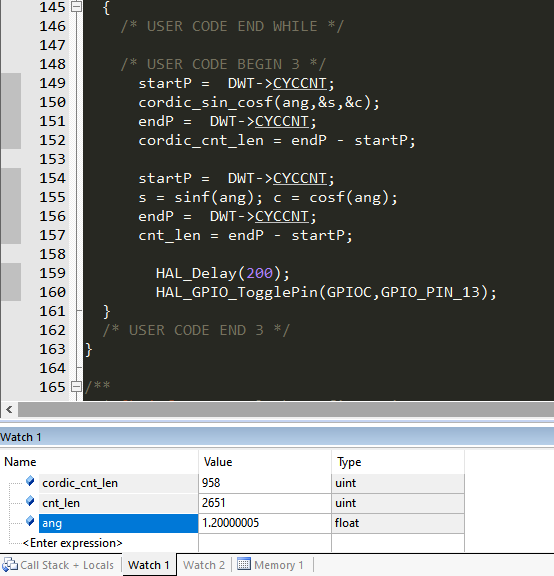
另外考虑到这个算法计算一次就输出两个结果，使用起来也相当方便。例如在Vectoring mode下旋转，可以同时计算出反正切和矢量的长度，相当于直接完成直角坐标系到极坐标系的转换