角速度计/陀螺仪误差模型
通常角速度计的真实值可以简单地用以下式子表示
其中A代表了尺度因子误差以及跨轴影响,b代表角速度计的偏置,其中包含了固有零偏,每次上电带来的随机偏差,温度变化带来的零偏。N则代表角速度计采样值的噪声,可以将量化噪声,角度随机游走以及零偏不稳定等归入此项。后两个也是角速度计两个重要的性能指标。
- 随机游走:角速度中的白噪声成分范围,单位同噪声系数
- 零偏不稳定性:在一段长时间内静止放置的角速度计可能的变化范围,一般用deg/h
通常情况下,在短时间的积分中影响计算出的角度的误差主要是偏置项,通常校准偏置有以下几种手段:
- 偏置设为固定值预先校准
- 上电后静止采样数据获取偏置
- 标定温飘曲线,即静止时温度与偏置的关系
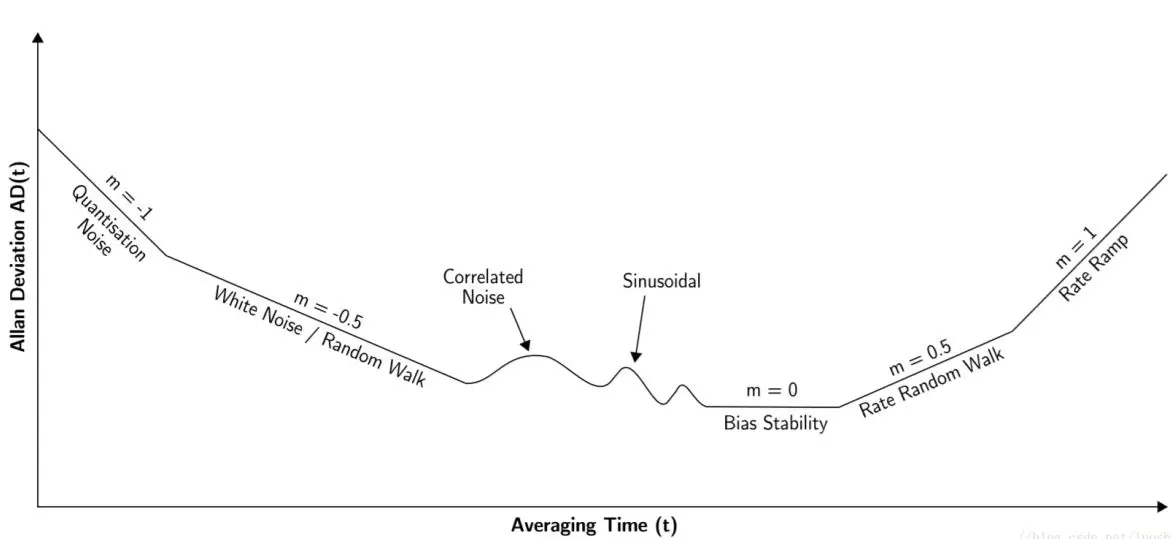
而长时间过程中随机游走和零偏稳定性参数对计算出的角度也有明显影响,可以用Allan方差评估,这里不作深入解释。
加速度计误差模型
针对加速度我们仅仅关注静态零偏,而不会过于关注积分后的误差,其原因是在姿态解算中加速度计往往被用于估计瞬时加速度的方向,而不会用于估计速度。真实值与测量值的关系可以简单地用以下式子表示
其中S代表尺度因子误差,C代表跨轴误差,前者应该非常接近1而后者应该趋近于0。b代表加速度计的偏置,N代表测量噪声。当然加速度计的噪声也可以用Allan方差评价,但是实际上使用中加速度计并不需要长时间的微小误差。
IMU校准
加速度计校准
加速度校准通常采用6面校准或者12面校准,一个恒定的重力加速度可以作为绝对参考,通过在三个轴上分别施加正向与反向的g可校准参数。在上述加速度参考模型中,尺度因子误差、跨轴误差以及偏置总共12个未知量,需要解12个方程。方程可以写成如下形式(这里与上面误差模型有点不同,其偏置需要乘以各个尺度因子)
但是六面校准中需要测量六组参数共18个方程,故需要抽取其中某些方程。这里以Pixhawk固件中校准加速度计的方法为例,六面校准有以下步骤
将IMU置于6个不同朝向的水平面(垂直于重力加速度的平面)上,使得加速计三个轴都有检测到+/-g方向的机会,即测得六组数据的参考值应为
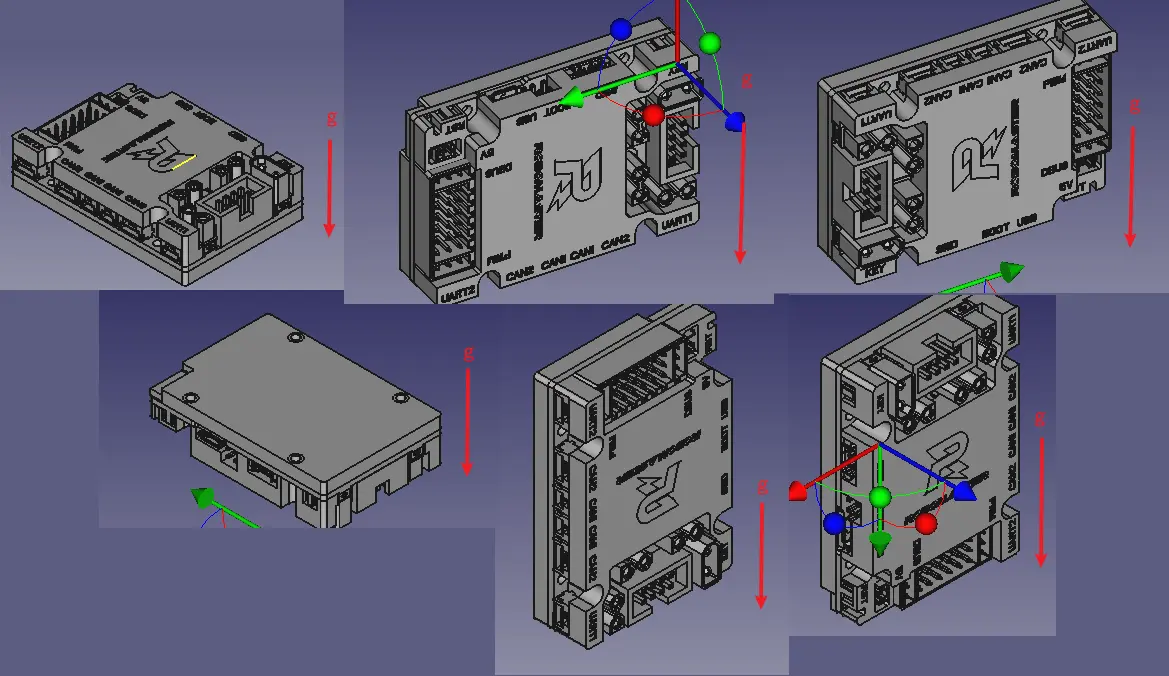
采集每个轴的数据一段时间求平均值,减少加速度计噪声的影响(实际上在这里加速度计的带宽可以大大放低,有助于采样值稳定)
先将求三轴偏置:假设加速度计正反向的尺度因子误差一样,那么+/-g采样值求平均即可消掉重力加速度求得偏置
三轴采样值减去偏置后得到无偏置的加速度,下一步是根据无偏置的加速度求得三轴的尺度因子与跨轴误差,抽取三轴中的其中一个重力加速度方向的一对采样值与参考值,代入2.1式中解方程即可
当然18组数据也可以用线性回归的方法求出12个量的解,上述方法只是用于简单校准。
考虑到水平面可能存在一定误差的情况下应该使用十二面校准,它在六面校准的每个面上增加多一个采样值,即将IMU垂直水平面旋转180度后得到的采样值与未旋转的采样值求平均,可以降低水平面微小倾斜带来的误差。其原理是当平面倾斜时采样得到的参考值应该是(以z轴为例)
而当在这个平面上旋转180度后得到另一个参考值,求平均得到
可以看到参考值被纠正为正确的值,而对原始采样值同样进行同样的操作即可获得更为精确的测量值。
角速度计校准
角速度计的校准相对简单一些,实际上我们更加关心角速度计的偏置,它对于积分出的角度影响非常大(虽然零偏也存在一定的随机性),尺度因子误差也有一定影响,但是在运动角速度范围不大的情况下误差可忽略(或者说,尺度因子误差只是影响动态情况下的角度漂移)。而加速度计的校准我们关心它测量重力加速度的方向的精度,因此尺度因子误差与偏置都需要校准。
考虑到温度对于角速度计零偏的影响,角速度计的校准方程可以写成以下形式
校准方法是测不同温度下的静止时的数据,然后线性回归拟合出零偏-温度直线即可,当然更加准确的方式是用高次的多项式拟合,但是大部分情况下线性补偿已经足够了。
除了上面这种温度补偿外还有一种方法是直接加热IMU至高过环境温度10°C以上并且闭环控制温度稳定(不通过制冷+制热双向稳定温度的原因当然是制冷不好实现,加热只需要几个电阻即可),这样直接可以完全避免温度对IMU的影响,但是高温下可能各种噪声可能会有增加,并且每一次启动后都需要等待温度稳定。
实际校准中也会遇到问题。以RoboMaster开发板C型上的BMI088的角速度计为例,其温漂与噪声几乎是在同一量级上,因此在拿到不同温度的采样数据后做拟合的散点图大概是这样的
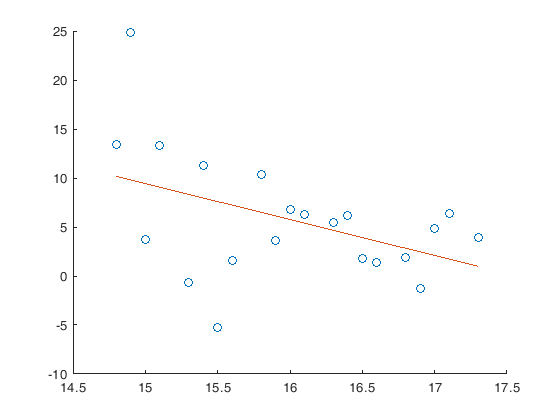
可以看到每个点的温度都很难收敛于直线上(当然也有可能是我的采样点数太少了),这个时候校准一个常量,后面交给解算算法动态校准即可。