IMU算法：序 | 姿态解算算法概述

姿态表示

姿态表示即为以大地为参考系下的坐标轴到机体坐标轴的旋转表示方法，其数学表示有如下几种

欧拉角

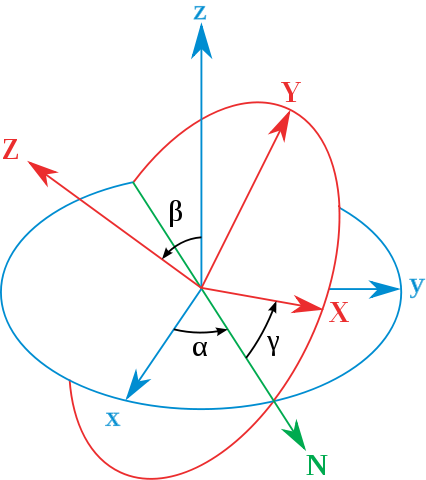
最直观也是控制中常用的姿态表示方法，三轴坐标系按照Yaw(偏航角)-Pitch(俯仰角)-Roll(横滚角)先后旋转对应角度得到。这种表示方法的缺陷是存在万向锁的情况，这种情况下有一个姿态的自由度会丢失

方向余弦矩阵(DCM)

即三维坐标轴的旋转矩阵，一个机体三维坐标系下的矢量左乘以该矩阵可以得到大地坐标系下的矢量，该矩阵R与欧拉角的关系表示为

通过对该矩阵求逆（实际上由于矩阵是正交的，因此求逆也等同于转置）也可以得到从大地坐标系转换到机体坐标系的矩阵

四元数(Quaternions)

被3Blue1Brown称作“外星人使用的东西”，四元数完全不符合人的直观上对于旋转的理解，但其优势在于没有欧拉角度的万向锁的问题。在具体表示某个向量v绕单位向量u旋转θ时，归一化四元数意义可以表示为

上面这里是将矢量v填入虚部组成一个四元数进行运算，这里四元数的乘法比较特殊。与矩阵类似，四元数的左乘和右乘不相同，左乘按照以下矩阵运算

而右乘则写为

两个归一化四元数的乘法的物理意义是两个旋转的叠加，正如旋转矩阵的矩阵乘法。当然上述旋转的过程也可以写成旋转矩阵的形式，根据旋转矩阵又可换算回欧拉角

同时其角度不直观带来的结果是角速度与四元数微分的关系并不如欧拉角明显，但是实际上四元数的微分计算也相当简单，其结果即为角速度乘以姿态四元数的1/2

据此可以采用一阶积分方法将IMU角速度计测量值积分为四元数

李代数so(3)

实际上，上述提到的几种旋转方式都是基于一个最基础的表示，即空间中的坐标系绕某一个轴旋转一个角度（或者说叫做轴-角的姿态描述），这样来看旋转应该是可以表示为一个三维的无约束变量。而上面的提到的单位四元数是一个四维的矢量，但是带有一条单位化约束，而九维旋转矩阵本质上也是三维欧拉角的映射，因此可以说旋转的表示只需要三维。而这种三维变换的旋转操作在数学上抽象出来的统一表述称为SO(3)旋转群(Special Orthogonal Group)，上面提到的旋转矩阵与单位四元数均在SO(3)定义中。SO(3)旋转群属于李群，其切空间为李代数。换言之上述的旋转操作可以与一个向量空间互相映射

纯数学的内容毕竟是抽象的，这里从工程的角度简单解释这种表达方式的意义。不论是四元数还是旋转矩阵，对于一个矢量的旋转操作都是乘法，并且两者实际上还要带着约束运算，这两点在信号处理里面实际上是不太常见的。我们最偏爱的，最常用的滤波算法都是线性的，而乘法（广义上的，四元数乘法也算乘法）本身则是非线性的，非线性在算法设计中是极其不讨喜的。一种消除非线性的直观思路是，用其他非线性的变换（或者说是非线性环节的逆变换）把非线性转回线性，对应这里的乘法我们希望把它变为加法，这样旋转本身就是线性的。
显然这里乘法与加法的互相映射实际上也就是我们常说的对数映射和指数映射，也就是上面提到的李群和李代数之间的映射。李代数so(3)这个三维向量空间也有十分直观的理解，三维矢量的方向代表旋转轴，而其模长代表旋转的角度。以旋转矩阵为例，SO(3)与so(3)之间的映射关系定义表达为

其中是的逆操作，即由反对称矩阵变为三维列向量。工程中例如角速度计的测量可认为是在so(3)上的旋转微分。四元数SO(3)与so(3)之间的映射关系就更加直观了，四元数的虚部也即旋转轴，实部为旋转角度一半的余弦。

姿态解算算法

IMU(六轴)中角速度计虽然能通过积分得到角度，但是测量中的零偏会让积分出的角度出现累计误差，而加速度计可以测量重力加速度的方向作为绝对参考的方向修正角速度计的误差，但是其测量噪声较大。由于两者均能够给出姿态信息，因此通过设计一个六轴融合算法，可以扬两者之长估计相对于地面的姿态，降低角速度计的零偏与加速度的影响。下面介绍两种常用算法

Mahony/Madgwick融合算法

Mahony/Madgwick算法是早期六轴与九轴融合使用最广泛的算法（论文&代码见文末参考链接），它计算简单，容易被移植至各种运算能力较弱的MCU平台。Mahony算法的思路是将重力加速度的偏差角度转换为等同于角速度计测量的角速度大小，再将其与角速度计测量值通过比例+积分融合计算总等效角速度，最后将等效角速度积分得到对应姿态。而Madgwick算法采用梯度下降法找到从加速度计数据代表的姿态旋转到当前姿态的四元数差值，将其与角速度即数据代表的姿态旋转的四元数差值进行线性插值融合。简而言之两者均采用的是线性的方式进行融合，但是Mahony融合操作的对象是角速度，而Madgwick操作的是四元数差值。以较简单的Mahony为例，具体过程如下

首先计算当前姿态对应的单位重力加速度方向

对当前姿态单位重力加速矢量与测量出的重力加速度值（已归一化）求叉积，得到两者旋转轴的单位矢量与旋转夹角的正弦值的乘积作为旋转误差值。

假设旋转误差极小，其正弦值约等于其角度本身，因此旋转轴的单位矢量与旋转夹角乘积即可等效为另外一个虚拟的“角速度计”测量得到的三维轴-角矢量。因此可以将其与角速度计测量得到的旋转角度作为误差，代入一个PI控制器得到修正后的补偿值。实际上，这样补偿等效一个带输出反馈的互补滤波器，其稳定性等分析过程在论文Nonlinear Complementary Filters on the Special Orthogonal Group中提到过

最终将补偿加上输入一起代入等式3四元数积分即可

Mahony算法的优势在于通过一个计算上足够简单的方法，很好地解决了IMU中Pitch与Roll零偏的问题，因此能够广泛应用。

Kalman(EKF)融合算法

通常作为一个足够全面的估计算法，Kalman滤波会根据模型同时考虑噪声与测量误差，一般融合的思路是将其中一个传感器值作为预测值（可以作为Kalman的外部控制输入），而另外一个传感器的值作为测量值，滤波器测量噪声方差与过程噪声方差可以根据某些约束条件进行调节。

Kalman相比于其他算法相对灵活，其状态量取值可以是四元数，DCM甚至是欧拉角。以A DCM Based Attitude Estimation Algorithm for Low-Cost MEMS IMUs中的算法为例，采用DCM末行作为Kalman的状态量（由于融合中Yaw轴平行于重力加速方向，因此重力加速度对其旋转没有任何修正参考，真正融合的是Pitch与Roll的角度），其通过角速度计预测的旋转值如下

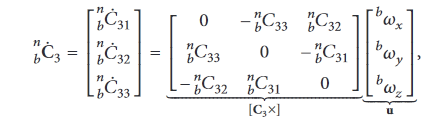
而DCM末行的物理意义是当前估计姿态下世界坐标系的重力加速度方向（可以这样理解，DCM矩阵乘以z轴单位向量，也就是世界坐标系下的重力加速度方向，得到当前姿态坐标系下的重力加速度方向），因此只要将加速度测量值作为状态观测值z即可构造完整的Kalman滤波。由于角速度计测量值转换到观测值的过程并不能用一个矩阵描述，因此实际该Kalman为扩展Kalman(EKF)

在加速度计测量中，测量值不等于一个g的情况下其置信度应该降低。论文中的DCM Kalman采用自适应的EKF很好地实现了这一点，即根据加速度测量值调节滤波器的R矩阵的值

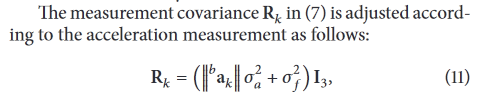
当然根据实际测量出的加速度的值与当前姿态的对应的重力加速度的值矢量相减，可以得到线加速度的估计。

需要指出的一点是，论文里面还提供了IMU角速度计的零偏估计，实际上是一个过程噪声Q矩阵极小的Kalman滤波，但是在高运动的场合下这种估计方法不可靠。

类似的思路在知乎专栏 - 从全状态观测器到卡尔曼滤波器（五）姿态解算中的应用与代码一文中提到过，当然我们也可以直接以为状态量四元数进行估计，省去在Kalman滤波器外对Yaw轴的积分，但可能会出现Yaw发散的问题

应用

零偏估计

实际上如果运行上面两种算法解算都会遇到一个问题，融合算法并不能修正Yaw轴角速度计积分带来的误差，Yaw轴几乎无例外地在静止条件下会不断漂移。

为了解决零偏带来的误差，通常会在算法里加入静止检测。当角速度计输出值极小并保持一段时间后可以认为IMU处于静止状态，并将静止条件下角速度计输出值经过滤波处理后得到稳定的偏置值，在下轮的算法中将角速度计测量值减去该偏置作为输入。

当然理论上用这种办法并不一定可以将零偏与实际测量分开来，因为实际测量的情况下也是可以有零偏大小的运动存在，但是对于零偏已经很小的IMU而言这种解决方法却是行之有效的

高运动检测

当前IMU采用的Kalman估计几乎无一例外地考虑非重力加速度的影响，这一点应该是针对Mahony算法而言。Mahony算法对于任何加速度输入都一视同仁，都只取方向而不关心其加速度大小是否合理。

可行的解决方案是在检测到高运动的场合时，仅仅依靠角速度计积分获得姿态，或者根据加速度大小动态调节Kp与Ki

商用算法

一般这一类算法可以自己编写并且调参以取得更好的性能，但是现在也不乏有些公开的商用算法库可用，它们一般是已经编译完成的二进制链接库，下面列举一些我认为比较好用的库

ST的MEMS算法库：MotionFX库中有针对六轴/九轴的算法，可免费使用
Bosch的BSXLite库：功能最完善但是参数私有，仅提供BMI160等参数输入试用，完整版参数需要付费
Invensense的motion_driver库：MPU6050专用的库，内部包含校准以及各种姿态解算