关于数字滤波器设计

原理

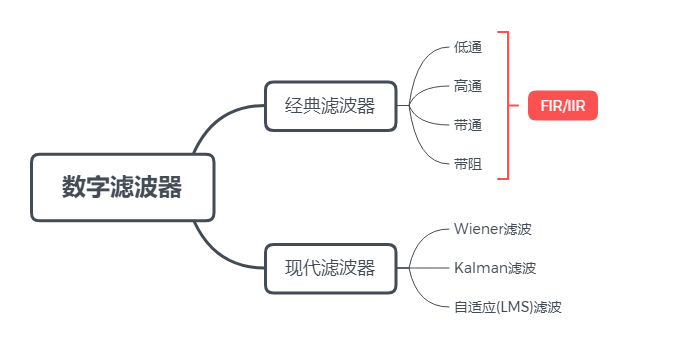
所谓滤波是指再输入信号中提取期望有效的信号，消除不期望的出现的信号即噪声。经典的数字滤波器主要利用信号的频域特性处理噪声，即滤除指定频率分量的滤波器。而现代滤波器利用的是信号的统计特性，即根据某个信号出现的概率进行滤波。这里主要讨论如何设计经典滤波器。

经典滤波器按照结构可以分为IIR（无限冲激响应）和FIR（有限冲激响应）两大类，前者存在输出反馈回路，可以用较低的阶数获得较高的选择性，但是相位是非线性的，并且在设计上存在不稳定的可能，而后者则恰好相反，无输出反馈回路，在同样的选择性下FIR滤波器需要较IIR更高阶数，但其相位是严格线性的并且滤波器总是稳定的。例如在对于控制反馈量的滤波，宜采用FIR确保其输入波形不发生失真。

设计

数字滤波器可以借助Matlab实现，这里以2阶低通IIR为例。打开Matlab的Filter Designer，在对话框内选Lowpass，Butterworth，指定阶数，通带阻带大小，点下面的Design Filter即可

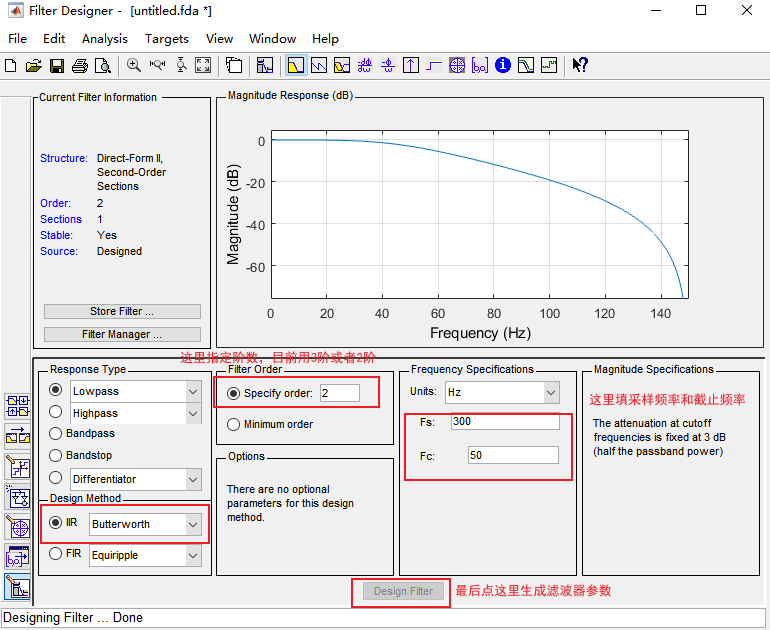
当然同样可以选择FIR滤波器，类型选用Window（窗函数设计法），Window选项选用合适的窗函数即可，参考下表

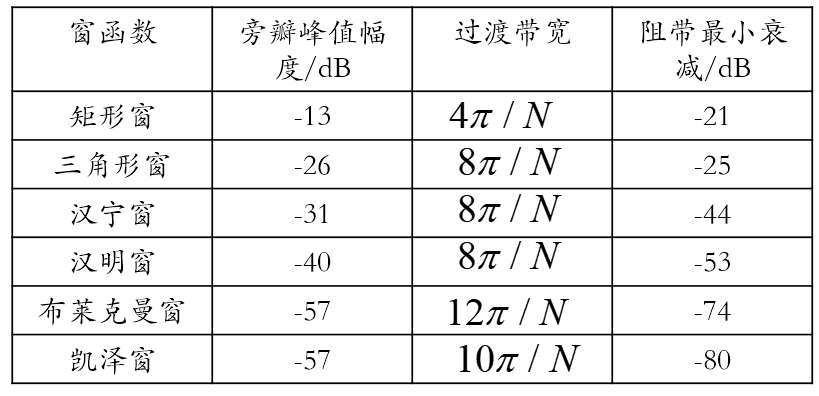
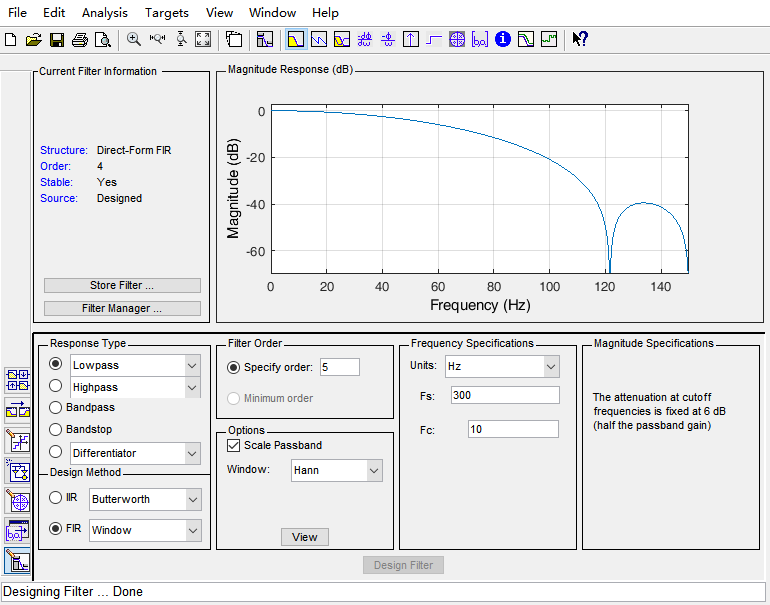
查看参数的作用也可以点工具栏上的Filter Specification

实现

直接计算

以二阶IIR实现为例，根据IIR的N阶差分方程

可以直接编程计算，但是Matlab生成的滤波器默认带多个Section，为了能直接计算，需要将参数转换为单个Section，在菜单栏中选Convert -> Convert to single section

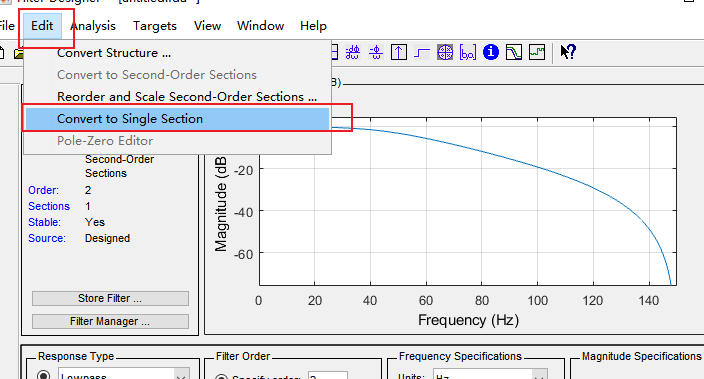
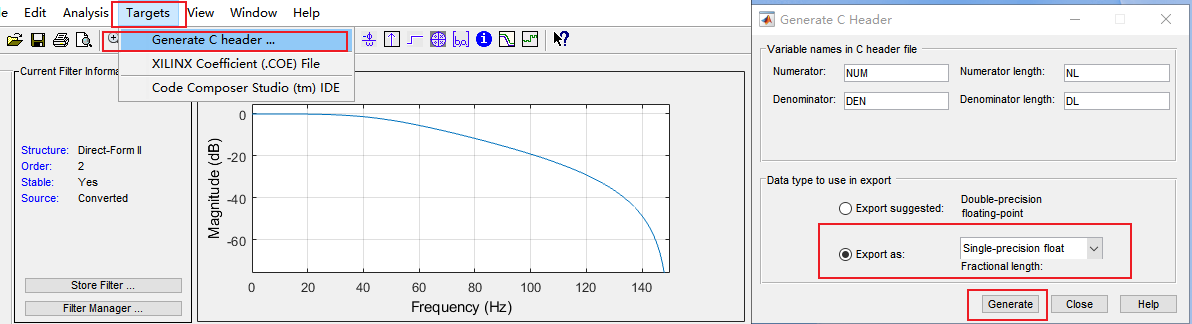
在Filter Coefficient中可以看到参数分为Numerator（分子）和Denominator（分母），这是写成系统方程的表述，分母代表ai(a0总是为1)，分子为bi。然后在点Generate C Header即可生成带参数的头文件fdacoef.h

实现代码

/**
  * @brief  2-order IIR filter
  * @param[in]  x    input in fp32
  * @param[in]  ch   input channel, there are MAX_FILTER_CH_2 channels available
  * @return output fp32
  */
float iir_filter_2(float x, unsigned int ch){
	static float y2,x2_n1[MAX_FILTER_CH_2],x2_n2[MAX_FILTER_CH_2]
					,y2_n1[MAX_FILTER_CH_2],y2_n2[MAX_FILTER_CH_2];
	y2 = NUM[0]*x + NUM[1]*x2_n1[ch] + NUM[2]*x2_n2[ch]
						- DEN[1]*y2_n1[ch] - DEN[2]*y2_n2[ch];
	y2_n2[ch]=y2_n1[ch]; y2_n1[ch]=y2;
	x2_n2[ch]=x2_n1[ch]; x2_n1[ch]=x;
	return y2;
}

FIR的实现类似，但是Convert Structure里面应选择Direct-Form FIR

ARM Math库实现

ARM官方提供了可在STM32上运行并且带优化的arm math库，其中就包含了各种滤波器函数的实现，根据精度不同可以使用多种定点和浮点计算，并且支持如下滤波器实现结构

IIR Biquad 串级
即Matlab IIR 设计里Direct-Form默认生成的带多个Section的滤波器，实质上是多个二阶IIR串联结构，其中针对单个IIR的结构支持Direct Form I（直接I型），Direct Form II Transposed（直接2型），在文档中提到的初始化直接型的参数说明
- Coefficient and State Ordering
  The coefficients are stored in the array pCoeffs in the following order:
  {b10, b11, b12, a11, a12, b20, b21, b22, a21, a22, ...}
IIR Lattice
即格型网络结构，对应Matlab结构Lattice Autoregressive Moving-average，文档说明的初始化参数为
- pkCoeffs points to array of reflection coefficients of size numStages. Reflection Coefficients are stored in time-reversed order.
{kN, kN-1, ..., k1}
- pvCoeffs points to the array of ladder coefficients of size (numStages+1). Ladder coefficients are stored in time-reversed order.
  {vN, vN-1, ..., v0}
需要注意的是Lattice的初始化参数其顺序与Matlab生成的顺序完全相反，在转换为代码是需要调换
FIR 直接计算
这个跟上面自己编程实现类似，但是与IIR Lattice的参数一样都是逆序的
- pCoeffs points to a coefficient array of size numTaps. Coefficients are stored in time reversed order.
  {b[numTaps-1], b[numTaps-2], b[N-2], ..., b[1], b[0]}
FIR Lattice
参数类似IIR Lattice 但没有ladder coefficients，参数顺序也是逆序排列

以三阶IIR Biquad 串级（浮点）为例，由于Matlab中生成的参数不符合输入要求，因此我们只能手动完成变换。在转换为Direct Form II 后选File-> Export，选导出到工作区

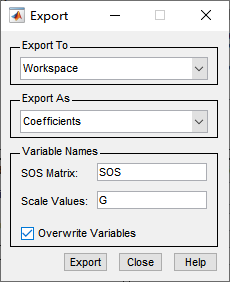
导出后可以看到工作区多了两个变量SOS和G，在CMSIS ARM Math库中没有把增益作为输入参数，因此只能预先合并入SOS中，编写Matlab即可获得C代码

m_array = reshape(SOS.*G(1:end-1),numel(SOS),1);
fprintf("const float Coeffs={");
for i = 1:length(m_array)
    if i == 1
        fprintf("%.11ff",m_array(i));
    else
        fprintf(",%.11ff",m_array(i));
    end
end
fprintf("};\n");

其初始化和调用应该是这样的

//初始化
arm_biquad_cascade_df2T_instance_f32 S;
const float Coeffs={0.00989732f,0.09510798f,0.01979463f,0.09510798f
    ,0.00989732f,0.00000000f,0.00989732f,0.09510798f,-0.01753881f
    ,-0.07701693f,0.00803332f,0.00000000f};
float state[4]; //2*numStages
arm_biquad_cascade_df2T_init_f32(&S, 2, &Coeffs, state);
//执行单次滤波
float input,output;
arm_biquad_cascade_df2T_f32(&S,&input,&output,1);

同理Lattice型只需要将输出数组顺序反转，用上述后半段程序转换为C数组即可