简介
当我们划分滤波器时通常会将其划分为至少两类,一类是经典滤波器,即针对频域滤波的滤波器,而后一类则是现代滤波器,利用信号的统计特性进行滤波,Kalman滤波则是这种滤波中的典型代表。
Kalman滤波的基本思想是构造一个使得信号测量值与预测值误差的方差值最小的滤波器,它同时考虑了信号测量中的高斯噪声,利用给定模型进行预测并修正输出。以单个变量的滤波器为例
通过调节K的大小可以调节输出中本次和上一次值所占的比例,当K的值固定时可等效为一个简单的FIR的滤波器。但Kalman滤波器的做法是,根据前后两个量的方差大小确定其不确定性,据此可以动态调节K的值,即更加相信哪一个变量
最终目的最小化预测与实际之间的方差,在上面这个例子中预测值相当于是上一次的x值
在Kalman滤波器中,根据模型获取信号值的过程称为预测(Predict),更新方差以及a(增益)的过程称为更新(Update)。由于预测模型不符合实际过程而产生的误差噪声被称为过程噪声(Process Noise),由于测量本身产生的噪声被称为测量噪声(Measurement Noise)
原理
假设某个系统的状态方程可以用如下方程表示
其中xk为当前系统内部状态变量,一般不能直接观测,x_k-1 为上一次的状态变量,u_k为外部输入系统的量,A,B分别为两者变换到系统状态的变量。而z_k为当前观测值,它可由矩阵H变换系统状态而来,w_k与v_k分别为过程噪声和测量噪声,其对应的方差矩阵分别为Q和R。
根据该状态方程构造状态观测器
设
Kalman滤波器的目标是通过求解一个用于计算后验观测值的K值/矩阵(Kalman增益)
使得后验观测方差最小,这一点即体现了Kalman最优线性估计的特性。把上述方程代入后验观测方差化简可得
当
此时后验观测方差P_k有最小值
最后总结起来,Kalman滤波器的过程是先进行状态值和方差的预测
后更新输出以及方差(矩阵P,Q,R均为方阵)
参数构造
上面提到的两个噪声方差的矩阵Q(过程噪声),R(测量噪声)为Kalman滤波器需要预先给定的参数,它包含了两个信号中所含的高斯噪声的方差大小,可以说它们两个分别代表了预测值与实测值不确定性的大小。
直观上理解,Q大R小,Kalman滤波器将认为模型预测值的不确定性更小,在滤波输出中会更加偏向于预测值,表现为受测量输入噪声影响小,但是收敛到测量值的速度变慢。反之,Q小R大,Kalman滤波器将认为模型实测值的不确定性更小,在滤波输出中会更加偏向于实测值,表现为受模型预测的影响小,受测量值噪声影响较大。
当状态量之间均相互独立时,Q为对角阵,每行分别对应某个状态的过程噪声。而当状态量之间非独立时,Q矩阵非对角位置对应某行和列对应两个状态的协方差,在kalmanfilter.net上对矩阵Q的解释中提到了离散噪声模型下通过状态转换矩阵A或控制矩阵B构造Q,以加速度的方差计算位移和速度的方差
用类似的方法同样可以构造矩阵R,其中也包含实测值本身的方差与实测值之间的协方差,但具体的值应该根据信号的的统计数据分析得出
进阶
上述Kalman滤波器仅基于可用线性状态方程描述的系统,然而现实中可能遇到一些只能用非线性函数表示状态转换的系统,这时就需要改进传统Kalman
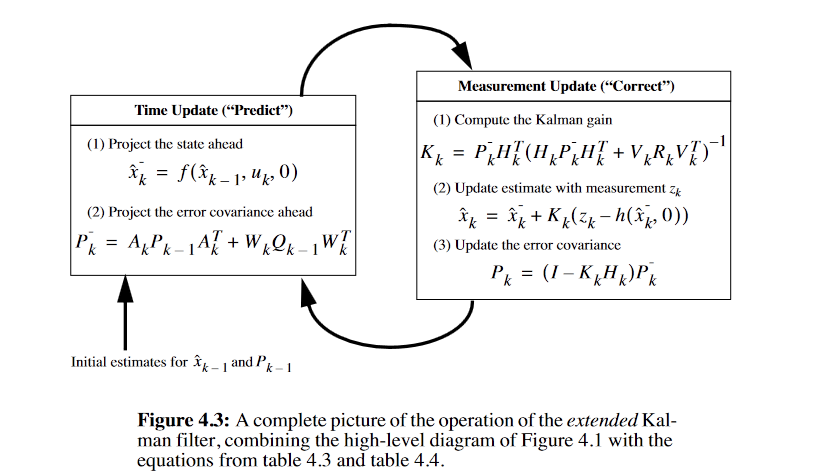
扩展Kalman滤波器(Extended Kalman Filter, EKF)
EKF的思想非常简单,它将非线性的模型通过类似泰勒展开的方式线性化,以此作为状态转换矩阵A以及观测矩阵H,同时由于两种噪声经过非线性的变换后高斯分布的方差将改变,因此还需要额外计算其变换矩阵W与矩阵V,其余过程几乎与Kalman滤波一致
无迹Kalman滤波器(Unscented Kalman Filter, UKF)
UKF解决非线性模型噪声变换的办法是通过近似非线性函数的概率分布(无迹变换),而不是像EKF通过线性化非线性函数。但由于目前大部分系统的非线性程度不至于将高斯分布完全扭曲,因此实际UKF与EKF的效果可能不会相差太大
参考
Kalman - A New Approach to Linear Filtering and Prediction Problems