搬砖笔记

SourceLizi's Blog

0%

RoboMaster弹道解算算法：电控实现

发表于 更新于 分类于 ，

RoboMaster比赛中，弹道解算是指根据视觉系统识别到的击打位置，计算云台应指向的角度的算法，这也是自动瞄准算法的最后一环。实际上相当于一个根据预测弹道轨迹反求瞄准角度的算法

理论计算

在视觉方案上计算的方案(1)(2)早已有人实现并被广泛使用，然而这两个算法均基于将弯曲的弹道补偿为直线，并且采用简单的迭代求数值解的思路编写。我认为这两个思路均比较奇怪，因为实际上在不考虑空气阻力的抛物体模型下非常容易求出解析解，而即使考虑了空气阻力计算出的结果也应与无空气阻力相近，另外迭代的危险之处在于可能存在计算失败的情况（数值上不收敛，或者方程本身是无解的）。针对这些问题，下面本文试图通过解析方法分别分析在无空气阻力模型和有空气阻力模型下求解发射角度的过程，以及一些边界情况的判定条件。

无空气阻力模型


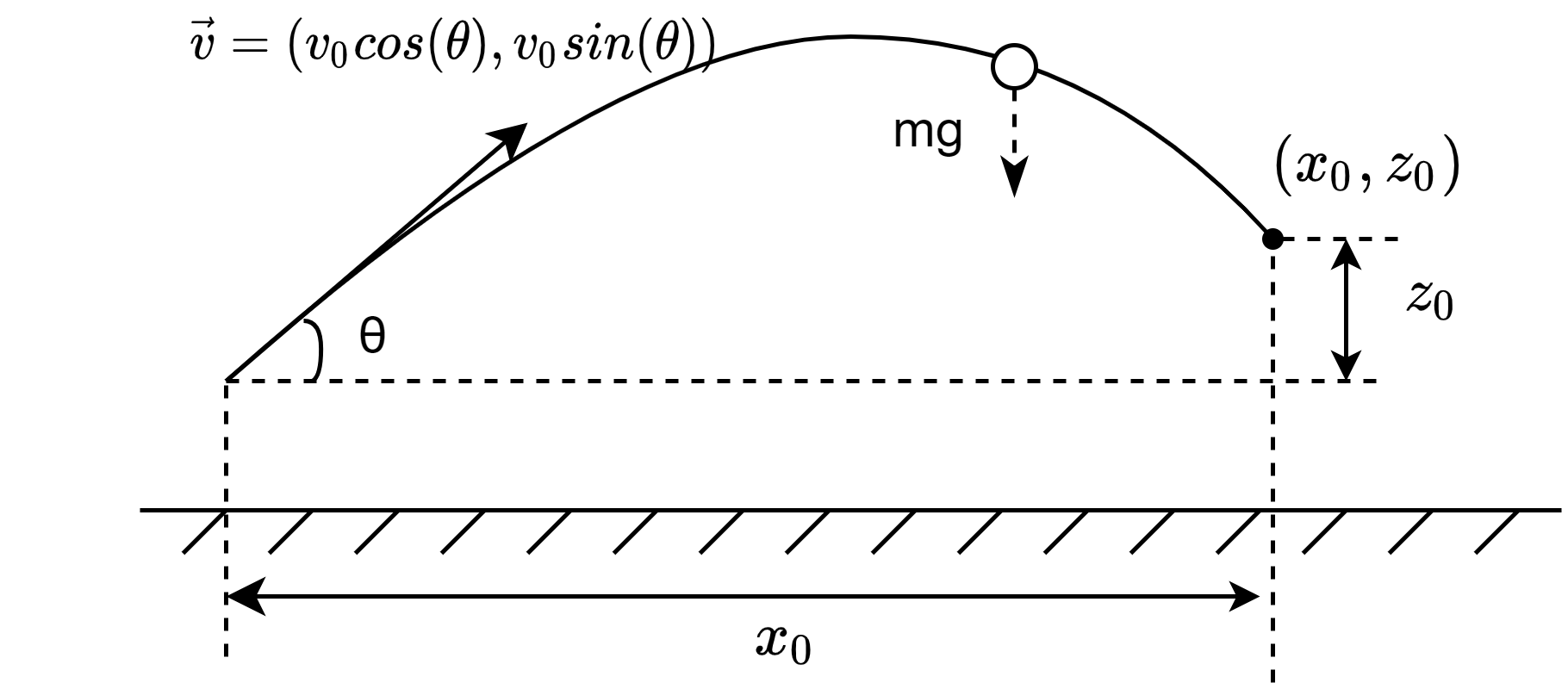
如上图，只考虑弹丸在竖直平面（沿重力加速方向）运动的情况，假设目标（图中实心圆）距离发射点x0，竖直高度差为z0。以初始速度v将弹丸发射，发射出去的弹丸（图中空心圆）仅受重力影响。可列出如下方程

消去第二条方程的t，并化简可得

令当

故该三角方程的两个解可以表示为

或

一次空气阻力模型

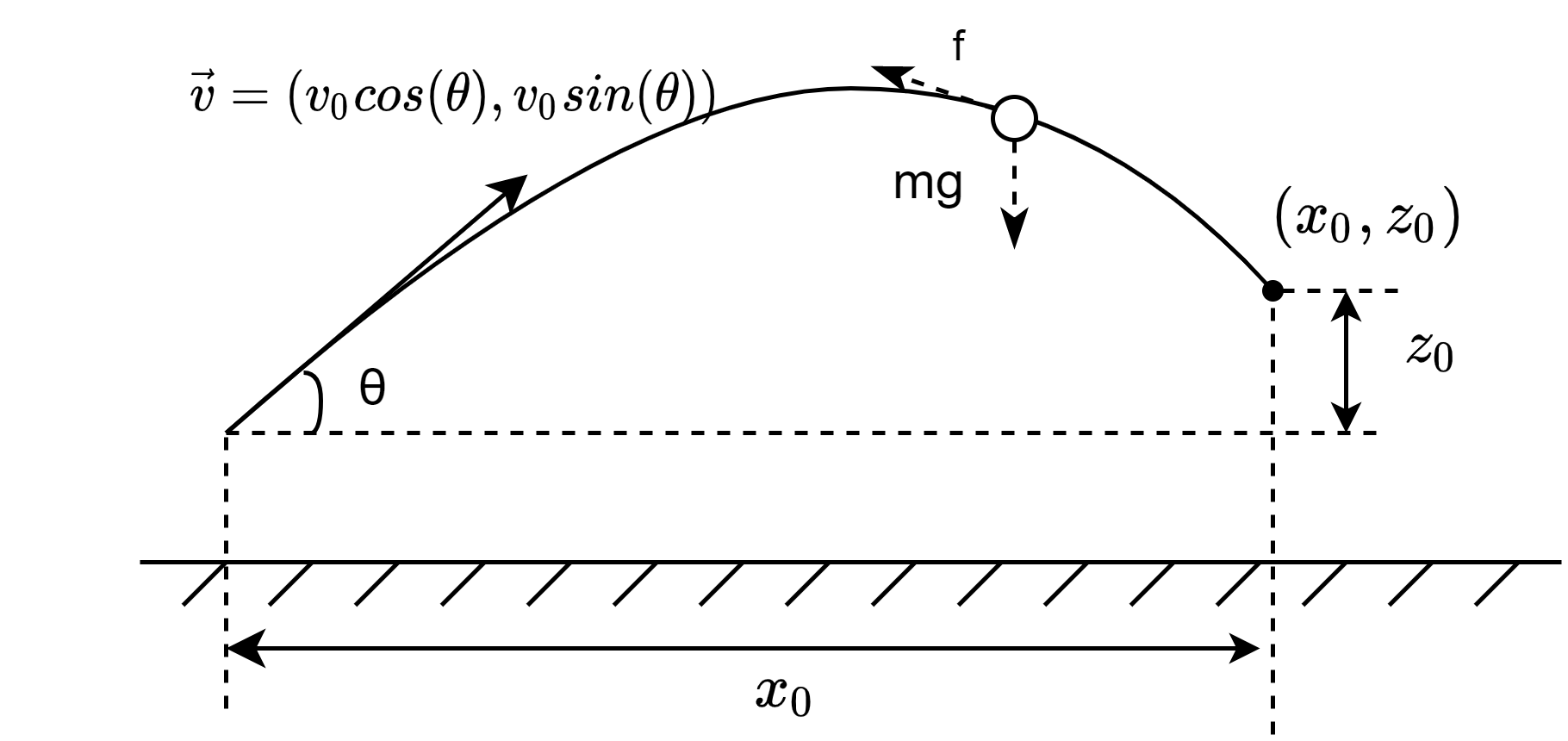
这个模型在上述无空气阻力模型的基础条件上，增加了一个沿速度反方向的空气阻力f，由流体力学相关知识可知，球形弹丸所受的空气阻力可表示为

其中C为球体阻力系数，ρ为空气密度，S为球体迎风横截面积。我们希望阻力可以简化为和速度线性相关，方向沿速度反向的力。当然这里只能做一个近似，后面的参数计算会提到实际上弹丸飞行时的雷诺数较大，基本上可视为湍流，故实际上弹丸的空气阻力与速度的二次方成正比。此处不妨利用(3)中的参数假设

其中k为近似的阻力系数，根据(3)中的推导，将其得到的解析解转换到当前竖直平面下的表示可得

同样地，消去第二条式子中的t并化简

当且时可得设函数令当时

其中正负号代表两段可能的求解过程，分别为θ为正角度或θ为负角度。上述求解过程即将求解角度θ的过程转换成求的过程。而该方程是一个超越方程，并无解析解，因此就可以采用上述的迭代方法求出其数值解。当然最常用的还是牛顿迭代法，简单来讲其迭代解t0的过程为

在经过迭代后得到的t0可通过等式求解θ，当然解也是有可能会存在两个的，稍后会提及如何处理多解的问题

二次空气阻力模型

这个模型是最复杂的，但也是目前来看最精确的。实际上到了这里求解基本上是需要完全依赖数值方法的，然而根据(3)(5)中提到的这个模型满足微分方程（在竖直平面内）


其中阻力系数满足

这个微分方程代表的系统比较复杂，但也存在关于时间t的解析解。比较麻烦的一点是，虽然已经将速度矢量分解为两个轴上的一元状态量，但是由于速度平方的存在，导致速度的符号在微分方程内丢失。因此实际上这个系统是存在两组方程的，区别就在于z轴由于空气阻力带来的加速度一项的符号反转，在(3)中可以知完整的解析解为

其中竖直方向运动分为了三种情况：第一种一开始速度向下，则微分方程只有一个且近似于于平抛运动，而第二种则是速度方向向上，即抛物运动的上升段。而第三种则是抛物运动的下降段，此处由于速度方向发生改变其微分方程改变的同时初始解也需要衔接上升段的方程。
逆向求解过程几乎与一次空气阻力模型中的流程相同，首先需要找到一个发射角度θ与目标距离的函数。这里的解析解看上去很复杂，实际上不妨假设，以及常量终端速度（即有空气阻力下自由落体的最终速度），由第一条式子可求出t，并将代入竖直方向运动的式子可得

这个形式看上去相对简单许多，但是对于求解来讲比较麻烦的一点是边界条件似乎比之前多，在下面一节会稍微讨论如何处理这些问题。比较幸运这里t的值可以用第一条式子显式地表达出来，因此以中间量代入z中可获得z关于的函数。求这一函数的根即为求解出命中该目标的值。同样地采用牛顿迭代法可获得方程的数值解

当然这里待求解的函数的导数也比较复杂，但同样地可以用中间变量的方式写开来

边界情况

针对无空气阻力模型，显然存在射程是否可及的问题，按照边界条件可以分为下面三种情况：


  • 此时方程有两个解，可以理解为进入射程范围内一个为顶点较高的轨迹而另一个为顶点较低的轨迹，在这个比赛中两个轨迹的实际区别在于，发射仰角是否在机械限位范围内，飞行时间一长一短，以及弹丸命中目标平面的法向速度不一样。实际上求解器需要综合考虑三个因素，选择其中一个解才能保证有效命中

  • 此时方程可以近似为只有一个解，这里用等号的原因在于现实中几乎不存在两边严格相等的情况，有解的条件下我们都认为是两个解，只不过此时两个解的角度十分接近，实际的物理意义可以理解为目标十分靠近射程的极限

  • 此时方程无实数解，实际的物理意义就是目标位于射程之外，不可能求解出一个可命中的角度

而针对一次空气阻力模型，显然存在空气阻力的情况下轨迹的可达射程范围至少需要满足上述无空气阻力模型。其次在推导过程中求解到的t0需要满足，否则方程无实数解。根据最后的两种表达式，可将情况分为两类

  • 假设θ<0有解，即一项为负号
    此时显然有，故单调递减，而，因此当时该情况下仅存在一解

  • 假设θ>0有解，即一项为正号
    对再次求导得到

    显然有,为凹函数，因此仅可能存在两个解，一个解以及无解的情况。判定是否有解的情况要根据的根以及是否落在内，并代入计算极值点判断实际解的个数。该过程运算较为复杂，因此该处解的判断可以交给无空气阻力射程与牛顿迭代法两个过程判断。直观上理解，无空气阻力射程范围内的点集合应该完全包括了有空气阻力射程范围内的点的集合，换言之只要无空气阻力下计算出不可命中那么有空气阻力模型也就无法命中
    当然实际情况几乎不存在处于射程极限的目标作为输入，这里也就不做过多讨论

最后针对二次空气阻力模型，情况变得更加复杂。边界除了在空气阻力下可达射程范围外还需要判断命中点位于上升段、下降段还是负竖直速度段(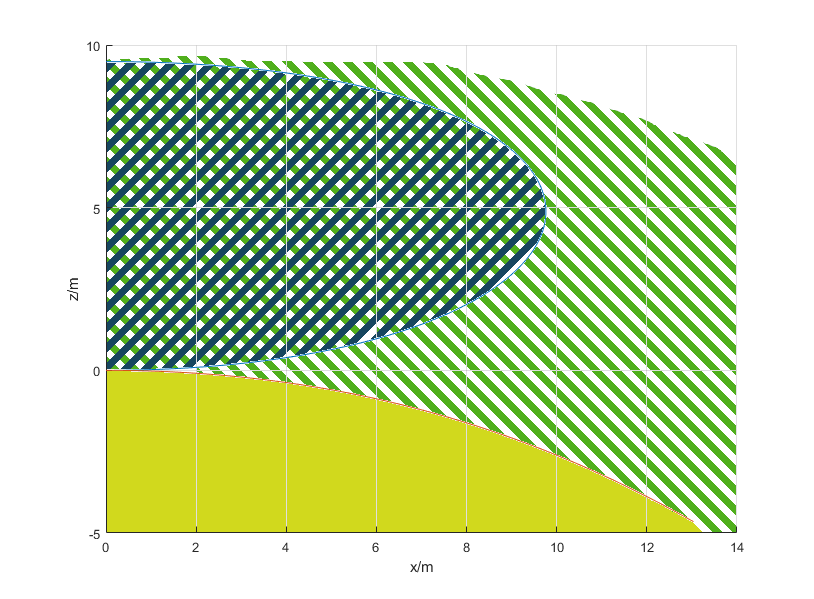)。射程范围的判断依旧需要依赖无空气阻力射程范围与迭代数值计算是否成功判断，最简单粗暴的方法自然是三段都迭代一次，看看哪次成功就得到哪个解。但是显然我们不希望在计算上浪费过多资源，尤其是在电控的平台上就更是如此。这里用图给出一个较为直观的理解（以，按照17mm弹丸阻力作为模型为例）

图中存在两条曲线边界，第一象限内蓝色边界为在不同发射仰角下运动轨迹最高点（即竖直方向速度为零的点）所连成的曲线，第四象限内橙色边界代表下的运动轨迹。直观上理解，最高点与原点之间存在若干条上升段的轨迹，这些轨迹只填满了图中深蓝色阴影的部分，二最高点的左下方可以视为存在若干条下降段的轨迹，这些轨迹将填满图中绿色阴影部分和黄色阴影部分，同理的轨迹只填满了黄色填充部分。这些不同颜色的部分代表了解的可能性。在已知目标点的情况下，，一个可行的求解角度的策略是

  1. 判断目标是否在橙色边界以下，即，若是，则以一段进行求解；若否，则继续下面一步
  2. 判断目标是否落在蓝色边界与z轴之间的区域内，即，若是，则以上升段进行求解；若否，则以下降段进行求解
  3. 若上述非下降段求解失败，则默认采用下降段再求解一次。若两者均不能求解，则说明目标在射程以外，求解失败
    当然上面边界的计算都涉及到代入的计算，这里以无空气阻力模型下的代入计算即可

参数测量

虽然上面理论分析可以推导出一个明确的结果，但是实际精确参数的获取就不会这么容易。下面列举求解器中常见的参数以及其测量方法：

  • 重力加速度g
    在国内一些地区可以按计算，误差不会太大。比较困难的是方向的获取，这个应该是要依赖惯性测量单元(IMU)获取，然而这个传感器的噪声和固定偏置带来的误差也不可忽视，在IMU | 误差模型与校准就提到这一点。当然在其他参量较为固定的情况下也可以手动在求解出的Pitch角度上加一个固定偏置，效果与IMU校准类似。
  • 阻力系数
    这个计算获得即可。常温20度下，取空气阻力系数为,空气动态粘度系数为，弹丸尺寸查规则手册可知分别为42.5mm和16.8mm，则两种弹丸在10m/s至30m/s范围内的雷诺数为

    查(4)中的表可知两者的阻力系数均大约在0.4至0.5之间，取。根据弹丸重量分别计算出二次空气阻力系数的参考值42mm弹丸, 17mm弹丸
  • 弹丸初速
    简单来看弹丸速度裁判系统的是可以直接测量的，但是作为已知量来讲求解需要先验的弹速。即使把测得的后验速度输入求解由于弹速的不稳定求解出的角度将一直抖动，这显然是不符合预期的。一般输入到求解器的速度是经过滤波（例如Kalman滤波），或者输入为固定值，通过外部其他手段控制弹速为固定值。但是想要精确估计下一发弹丸的速度来确保命中相对而言比较困难。在后面我们讨论弹速对命中率影响的问题是将其转化为求解确保能够命中目标的弹速散布。
  • 距离
    RoboMaster自动瞄准的经典问题就是距离测量，当然由于这部分是视觉系统的工作这里就不展开说了，大量可供参考的方案如单目/双目测距，激光测距等

误差分析与优化

从实践的结果来看大部分情况下采用无空气阻力的弹道就足够了，两个模型明显的差别会出现在超远距离的发射中，换言之弹丸飞行时间越长越容易受到空气阻力干扰。而引起误差的主要因素主要源于机械发射装置的不理想等因素，大概可以列举如下的几个误差来源：

  • 弹速计算误差
    前面已经说过，弹速的误差几乎不可避免，只能将其限制在一个较小范围内。例如根据上述无空气阻力的模型，可简单估计弹速轻微变化下的大小

    若为一块小装甲板的高度，上述问题就可以视为击中一块竖直放置的小装甲板所需要的速度范围，例如假设首先可求解得到,则代入上述关系式可得，代入小装甲板的高度可解得，于是弹速对命中率得影响可以转换为更加容易通过测试获得的弹速的的分布概率问题
  • 机械结构失配
    这个算是一个大类的误差，主要包括发射出去的弹丸自旋改变气动引起的偏移，弹丸尺寸公差引起发射参数的变化，发射后的弹丸与枪管碰撞引起速度方向的和大小的轻微变化等，这些在实际分析中想要建模分析非常困难，因此只能从机械设计上尽量保证降低这个方面的影响
  • 控制云台控制抖动或漂移
    实际上由于发射过程中的后坐力以及机械参数的不理想，云台的Pitch和Yaw可能会在瞬间产生一个力矩，或者说在没有发射装置的干扰下控制上就是不能稳定瞄准。这部分就属于电控云台控制的问题，在控制算法上将误差降低至可接受范围内即可
  • 其他误差
    这部分所占比重较小，包括上面提到的重力加速度测量误差，以及短距离内影响更小空气阻力系数的变化，风力风向等其他可忽略的因素。对于远距离的发射应采用有空气阻力的模型以减小误差。

还有一点这个模型并没有考虑移动目标的预测以及发射延迟，实际上在(2)中有一种较为简化的模型，将目标相对于发射点的速度等效为沿距离矢量r的速度与垂直距离矢量r速度的合成，将前者加入到等效子弹相对目标飞行速度，而后者者则采用求解出的子弹飞行时间预测Yaw轴角度。当然采用迭代法也可以，不过需要验证上述提到的有无解的情况。

求解器实现

仿真与验证

为验证上述算法的正确性，将在一定角度上计算出的轨迹代入求解器求解，将求解器的输出再输入计算出轨迹，查看是否经过该即可。拿其中仿真的轨迹画图可得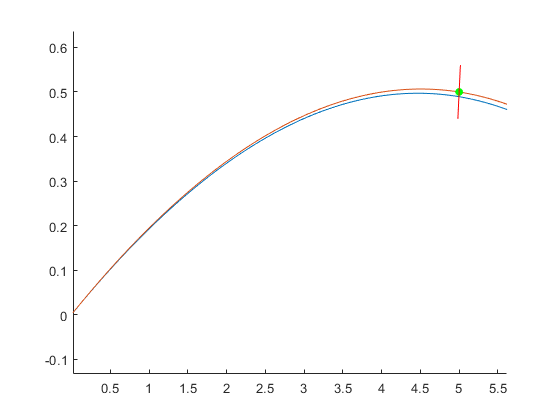

图中绿色点即为设定的目标，目标点上的斜直线即为装甲板的垂直高度范围。轨迹模型采用二次空气阻力模型，红色轨迹代表二次阻力弹道求解角度仿真的结果，而蓝色轨迹代表无空气阻力的仿真结果。在仿真中随机拿一些点测试发现，在仰角不大且飞行时间不长的情况下，无空气阻力和有空气阻力求解并不会有很大的区别

性能优化

不要忘记这个求解器需要在嵌入式平台上实现，实现上的最大压力来源于实时性。按照原始公式计算的复杂性不一定能满足实时性，尤其是有空气阻力的迭代。根据二次阻力求解器仿真的测试数据，对于初速度为15m/s，最大飞行时间为1.5s轨迹上上所有点集的数据求解结果来看，平均需要迭代3次（实际上是两次，最后一次用于计算误差满足要求，故按照计算量看还是3次，下同），最坏情况下可能需要迭代6次。故在真正实现上还需要采用以下几个技巧完成对每次迭代性能的优化

  • 储存重复变量
    简而言之就是减少对数值的重复计算，实际上在计算过程中有很多变量可以直接重复利用，或者根据已有变量经过简单的计算后转换得到，尤其是二次空气阻力模型下的迭代计算
  • 初始解的选择
    这种优化方法比较通俗的讲法是，如果你能够在迭代前几乎猜中实际解，那就可以几乎不用迭代得到精确结果。实际上牛顿迭代法的初始解数值上越靠近实际根，求解迭代的次数就会越少。选择一个好的迭代的初始解可以达到提升算法速度的结果，而且很可能是巨大的提升。由于这里实际上较小，不妨假设有无空气阻力求解发射角度之间的偏差较小，则迭代的初始解可设定为无空气阻力。计算出的角度实际验证最坏情况下（飞行时间接近1s,数值误差小于10^-5m）大约迭代6次之后就能确保得到正确结果。另外由于方程直观上应该有两个解的，这样取还能够确保迭代时能到一个确定的角度上，而不至于在两个解中间迭代出现不稳定
    当然这个算法对于远距离或者大角度的求解效果不太理想，我认为仍然可以通过改进初始解的计算来降低迭代次数
  • CORDIC算法
    这个在之前的一篇文章中也提到过。这个算法除了速度上可以与数学库的计算媲美外，最大的好处同一个计算过程可以同时得到两个结果，例如同时得到矢量(x,y)与x轴夹角和长度，或者同时得到某个角度的正弦值和余弦值等。恰好在这个求解器里这些超越函数计算也是成对出现的，如正弦/余弦，双曲正弦/双曲余弦等。因此我相信如果采用CORDIC计算性能会有所提升。
  • 利用时间相关性
    如果不是目标的切换的话，前后运算得到的解应该十分相近，利用这一点可以将上一个时间产生的解代入当前时刻中，降低迭代的次数。另外一点，实际上瞄准的过程并不需要得到一个瞬间精确的结果，因为云台等机构移动是需要时间的，因此若目标静止或者连续运动在每个时间片上，以上个时间片的计算结果作为初始解，进行有限次数的迭代。这样只要收敛的速度远远大于云台响应的速度，那么应该和瞬间计算出结果没有太大的区别。

示例代码

前面提到，无空气阻力的求解器能够应付绝大多数的情况，下面给出其求解器函数的示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#define GRAVITY_G 9.7833f
#define M_PI 3.1415926536897932384626f

typedef struct{
	unsigned int solution_num;
	float ang_solution1;
	float ang_solution2;
}ballistic_sol_t;

typedef struct{
	float x0,z0;
}target_spec_t;

void projectile_solve(float v0, target_spec_t* target, ballistic_sol_t* solution){
	float x0x0 = target->x0*target->x0;
	float distance2 = x0x0+target->z0*target->z0;
	float distance = sqrtf(distance2);

	if(v0 == 0.0f || (target->x0 == 0.0f && target->z0 == 0.0f)){
		solution->solution_num = 0;
		return;
	}
	
	float a = target->z0 + (GRAVITY_G*x0x0/(v0*v0));
	if(a > distance) {
		solution->solution_num = 0;
		return;
	}
	float alpha = asinf(a / distance);
	float phi = M_PI/2;
	if(target->x0 != 0.0f) phi = atanf(target->z0/target->x0);

	solution->solution_num = 2;
	solution->ang_solution1 = (alpha+phi)/2;
	solution->ang_solution2 = (M_PI-alpha+phi)/2;
	return;
}

输入参数包括速度弹速v0，目标位置参数target_spec_t，以及用于储存返回值的ballistic_sol_t结构体。ballistic_sol_t结构体包括了解的个数以及具体解的数值

参考

(1) RoboMaster OSS - 迭代弹道模型
(2) rm-controls - 枪管角解算器
(3) Github - jburguete/ballistic
(4) Drag on Spheres
(5) NASA - Flight Equations with Drag （此处下降段的阻力方向计算有误）
附弹道轨迹仿真 ballistic_sim.m