搬砖笔记

SourceLizi's Blog

0%

常见数值算法总结

发表于 分类于

方程求根

最简单的方程求根的问题可以描述为求令成立的的数值解，有以下几种常见方法

二分法

二分法是基于数学上根的存在性的条件，即若则在区间内至少存在一个根。二分法通过每次取根存在的一半，判断根存在于左半区间还是右半区间(\frac{a+b}{2},b)，确定根存在的区间后再重复上述步骤搜索缩小后的区间。不断重复即可不断缩小搜索范围，当这个范围足够小时我们认为它是一个点，即找到了对应的根。
二分法在区间取值正确的情况下能够保证线性收敛，但是其缺点也很明显，就是收敛速度太慢了。对于选的比较宽的初始区间需要非常多次迭代才能够达到较为理想的精度。

不动点迭代

这个过程比起二分法更加简单，若方程可以表示为则称后者的根为方程的不动点。对于给定的初始解，不动点的迭代表示为

不动点迭代方法也是线性收敛的，但是对于函数有要求，在根处需要满足不动点迭代才会收敛至此处。

牛顿法

对于函数假设其根，将函数近似为线性的，则在附近某一点处近似满足

这个过程写成迭代的即为牛顿法的表示。牛顿法可以说是所有迭代方法里面收敛速度最快的，在单根附近的收敛速度为平方收敛，而重根的情况下也能够有线性的收敛速度（当然如果已知为m重根的话可以把步长放大m倍，同样可以达到二次收敛的速度）。缺点除了需要计算导数外，存在导数为0的点时迭代不能够继续。多元函数的优化算法也会用到牛顿法，其情况会更加复杂在一些下面也会提及。

线性方程组求解

求解线性方程组即，可以说是最为常见的求解问题之一。在理论上考虑方程是否有解主要看矩阵是否可逆，而实际的数值求解中还要考虑求解的稳定性，即数值上的微小误差能否在计算中被忽略。如果对于系数矩阵其参数发生极其数值上微小的变化时，方程的解发生相对而言极大的变化，则该问题数值解的稳定性将非常差或者说难以精确地求解，我们称该问题为“病态的”(ill-conditioned).判断某个线性方程组求解是否为病态问题可以通过系数矩阵的状态数判断

这里的矩阵范数一般取无穷范数。其实际意义为参数微小变化引起在上相对变化放大倍数的上界，过大的状态数代表该问题极有可能是病态的，数值上难以求出正确的解。

以下列举的是线性方程组的数值求解方法，其中高斯消元法等用于对小规模线性方程组求解，而迭代法则适用于系数矩阵规模较大时的求解。

高斯消元法与LU分解

高斯消元法的基本思想与手工解线性方程组是完全一样的，即对n条方程消去其中某条方程的前n-1个未知数，从而求解第n个未知数，这样原来n个未知数的线性方程组变为n-1个未知数的线性方程组，重复上述消元步骤直至方程组的n个未知数完全被求解。矩阵形式下可以看作是消去矩阵的某列的n-1个系数，使得为上三角矩阵，例如对第一列进行消元

再用第二行中第二列之后的系数进行同样的操作消去第二列的系数，最后从矩阵最后一行往上回代可逐个求解出.
LU分解则是把上述对系数矩阵消元的操作写为一个下三角矩阵L，而消元结果则表示为上三角矩阵U，得到。这样线性方程组可以转换为，先求解方程再求解方程
高斯消元法与LU分解的方法计算复杂度较高，但是相比于真正意义上的数值算法，它求解的更加像是方程组的“解析解”，即能够用符号直接代表求解出的，但是规模较大的的方程组其计算量和所需储存空间均较大。因此高斯消元法与LU分解等方法较为适合求解小规模的线性方程组

迭代法

首先迭代法中首先最基础的是Jacobi迭代法。Jacobi迭代法可以认为是不动点迭代法的线性多元求解版本。在给定初始解条件下，每条方程改写为用和其他n-1个未知数表示第i个未知数的形式，代入初始解得到第i个未知数的迭代解。对每个未知数进行该操作后将迭代解作为下一轮的初始解，重复上述步骤直到收敛。将矩阵对角元素、分解的上三角和下三角矩阵表示为，则Jacobi迭代法的迭代式可以表示为

与不动点迭代法一样，上述迭代法也存在收敛条件，收敛条件为系数矩阵严格对角占优。严格对角占优的含义是，矩阵对角线上的每一个元素的绝对值均大于该元素所在行的其他元素的绝对值之和，即对任意，有
由于Jacobi迭代法存在收敛较慢的问题，其改进的方法有Gauss-Seidel法和逐次超松弛法(SOR)法。Gauss-Seidel法将每一步迭代的第i个未知数的结果代入后面n-1个未知数中，即Jacobi迭代法是经历一轮迭代后再更新迭代式中的，而Gauss-Seidel法则是在本轮迭代中只要计算出一个未知数的解析解就将其代入下一个未知数的迭代式中。其迭代式可以表示为

逐次超松弛法(SOR)在Gauss-Seidel法的基础上增加了对上一次的值的加权平均，即对方程组中的其中一个未知数，设Gauss-Seidel法的输出值为，则SOR法输出的迭代值可以表示为

其中为松弛因子。时该算法退化为Gauss-Seidel法，当的情况被称为超松弛，此时迭代速度将进一步提升，但是迭代值可能存在过冲，反而增加了迭代的次数。通过调整松弛因子可以控制迭代速度，当然也存在一个最优的松弛因子使得迭代次数最少。

无约束极值优化

最小二乘法

作为最简单的求解极值方法，最小二乘法能够给出取得最小值时的显式解，就如同一元函数中对一个二次函数求导后解线性方程得到最大值或者最小值的点一样。根据矩阵求导法则对求导并令其等于0可得

若可逆，则取最小值的.最小二乘法的意义在于它能够找到可能无解的方程的“最接近”的解，这个解也能够通过线性的形式表达，可以说是极值优化里一个特例。对于一些非线性的求解或者较大规模的线性求解，都是通过数值迭代的方法去逼近，下面将其分为线搜索方法和信赖域算法。

线搜索算法

线搜索指的是一类通过求解每次下降所需要的方向和距离，得到作用在自变量上迭代的步长。简单来讲就是可以写成形式的迭代算法都可以算作线搜索方法。线搜索方法主要是将问题聚焦于步长的获取上，该过程可以采用Armijo准则判定是否产生足够的下降。对于

在满足该准则的能够令下一步迭代保持下降。这个准则用数学语言描述了求解最值过程中的走出令函数值下降的步长应该满足什么条件（虽然每一步都满足上述条件能够不断下降，不一定能够找到全局最优解，但是不论如何最终都会得到一个相对的局部最优解）。而具体步长的计算也有很多种方法，以下列举一些常见的线搜索及其改进方法。

梯度下降法

如果对函数采用一阶近似，有

令为代表下降方向的归一化矢量，下降距离为标量.如果要让目标函数尽可能多的下降，那么需要令尽可能小，若只考虑方向的话也即令尽可能小。而这一项可以认为是梯度矢量和下降方向矢量的点积，当两个单位矢量方向完全相反时其点积应该是最小的。于是可以令，其迭代式写为

这就是梯度下降法(Gradient-Descent Method)的表达式，部分写法可能将梯度归一化与预设参数合并为一个参数，表达式里只有一个梯度。当然梯度下降法的参数也可以通过计算得到，在下面“共轭梯度法”中将步长距离作为另外一个求解的参数，优化出最大下降的距离。这个改进后的方法被称为“最速下降法”(Steepest Descent Method)。
梯度下降法作为一种简单的迭代数值方法被广泛用于包括机器学习的各种优化问题中。对其主要的改进包括动量法（简单来讲就是对每一步迭代的梯度进行一阶低通滤波，提高其稳定性），以及上面提到的参数虽然一般是人为设定，但是通过设计自适应的参数也能衍生出各种方法。常见的基于梯度下降改进的算法例如SGD,Adam等。

共轭梯度法

共轭梯度法(Conjugate Gradient,CG)主要用于求解由对称矩阵构成的二次型优化问题即

对其求导并且令导数为0可得极值点满足。也就是说，求解该二次型的极值等同于求解线性方程组的解。我们当然可以直接的方法例如高斯消元法计算线性方程组的解。但是在求解较大规模的问题时这些方法速度都不尽人意，这个时候就可以通过数值迭代的方法求解。而共轭梯度法就是求解这个方程的其中一种方法。
共轭梯度法与梯度下降法十分类似，首先考虑在给定第k步线搜索方向的情况下计算最优的下降距离，也即迭代时走这一步能够尽可能地走出最小值。设第k步步长距离为，残差，则优化问题可以表示为

当时取得最小值，这就是在给定方向的情况下的最优步长。
而如果考虑上下降方向的问题，可以直接设定，这个方法被称为“最速下降法”。但是这个方法的问题在于，其下降方向的一些分量是重复的，导致其迭代次数看上去增加了，我们希望它迭代一步就能够走完这个方向上所有的距离。一个简单的想法是，令不同迭代的方向矢量都是与矩阵A正交的，即。很容易联想到用G-S正交化过程来完成，利用给定的基向量计算当前迭代过程的方向表示为

不过这个正交化的过程需要储存之前所有步的下降方向矢量，这又增加了储存空间。实际共轭梯度法中是选择残差作为G-S过程构建的基向量，这样可以利用残差与之前所有下降方向正交，消去几乎所有的，最终下一步的搜索方向可以表示为

共轭梯度法的一种改进是，通过方程两边同时乘以另一个矩阵，降低系数矩阵的条件数提升共轭梯度法，这种方法被称为预条件共轭梯度法(Precondition Conjugate Gradient,PCG)。

高斯牛顿法

按照线搜索的基本思想，即找到一个能够使得下降最大的步长。这个问题可以进一步转换为一个最小二乘问题，即对于第k步迭代，最佳的步长求解的数学表示为

对函数进行一阶泰勒展开可得

其中，这样上述最小二乘可以转换为线性形式的最小二乘，

上面提到过，这类最小二乘法一般是有显式解的，在可逆的条件下有

使用完成迭代，这就是高斯牛顿法(Gauss-Newton Method)的整个迭代过程。当然，这个迭代过程也有几个很明显的缺点，在奇异的情况下这个算法就会失效。另外如果出现较大的步长的话一阶近似会出现不精确的情况，算法也可能不会收敛。针对这些不足之处，增加了各种改进的高斯牛顿法： Levenberg-Marquardt法(L-M法) 被提出。首先为了确保能够避免奇异，加入正则化参数，且

矩阵D一般取对角线上的元素构成的对角阵或者单位对角阵。
的取值实际上决定了这个算法是倾向于高斯牛顿法还是之前提到的梯度下降法。若D取单位对角阵，当时其迭代式与原始的高斯牛顿法一致，而当远远大于矩阵中任意元素时，也即后者可忽略的情况，这个迭代式就会变成梯度下降法的迭代式。通常在远离最优点处采用高斯牛顿法，而越接近最优点则换用梯度下降法确保能够稳定迭代到该点上，这个切换的过程就是通过不断增大实现的。
针对较大步长一阶近似不精确的问题，L-M法引入信赖域算法解决，即直接在原目标优化问题上增加约束，限制每一步的步长大小

至于如何求解带约束的优化问题，在后面一节“有约束极值优化”将会提到。

牛顿法

牛顿法求极值实际上相当于求方程的根，上面提到的一元函数的牛顿法修改为多元形式即对换为矩阵函数的导数，牛顿法的迭代式可以表示为

其中我们一般称为Hession矩阵，下面许多改进都是围绕Hession矩阵带来的问题来展开的。首先最致命的一点是若Hession矩阵非正定则会出现迭代方向违反，换言之迭代方向就不会朝着下降的方向进行。另外同时可能会出现Hession矩阵奇异的情况，无法求逆导致该方法失效的情况。即使Hession矩阵取值合适，其本身以及求逆的计算量也可能较大。针对这几个问题，下面衍生出牛顿法的两种改进

阻尼牛顿法

阻尼牛顿法可以看作是缩减步长的牛顿法。它为步长增加系数，确保每步都是沿优化方向单调（即符合Armijo准则）。令，阻尼牛顿法的迭代式为

当然比较典型的做法应该是不需要设定衰减的参数，而是使用回溯线搜索(Backtracking line search)的方法找到最佳的步长衰减即

拟牛顿法

针对Hession矩阵的逆直接求解难的问题，拟牛顿法(Quasi-Newton Method)系列的思路是通过间接的方法估计Hession矩阵替代掉二阶导数。对梯度进行泰勒展开可得

拟牛顿法的关键在于如何通过和求解Hession矩阵，或者说在进行最值求解的迭代之前，先再用数值方法求解出近似Hession矩阵的逆矩阵。其中比较常用的具体算法有DFP,BFGS以及通过迭代求解Hession矩阵的L-BFGS，其基本思路都是求解一个满足的正定对称矩阵的近似解。以最常用的BFGS为例，其对Hession矩阵的估计为

信赖域算法

将优化问题拆分为一块局部区域上的优化问题，这块小区域就是所谓信赖域。对于某些非线性函数来讲，通常其数学表示在全局上可能时非常困难的，而在局部小范围内是非常有可能表示为一个线性或者二次型的优化问题，这就可以利用上面提到的几种方法来完成子问题的优化。而且这样简化之后问题的求解难度大大降低了，单个步长的求解速度也会有所提升。上面提到的带约束的高斯牛顿法可以算作是一种信赖域优化算法。但是与高斯牛顿法不同的是通常我们会利用函数的二阶泰勒展开，即对于优化问题，我们将其拆分为给定的局部范围内的步长求解问题即

对上述式子求导并令其等于0可以得到到达极值点步长满足的方程，这样就将其转化为线性求解问题，可以采用上面提到的如共轭梯度法求解。另外，我们可以根据近似情况进行调整，即当出现优化后的则说明近似不正确，需要缩小信赖域重新计算。

有约束极值优化

非线性约束优化问题可以说是不限于线性的通例，可以表示为以下形式

显然对于上面两种约束，等式约束是对问题的降维，可以认为是规定了的一条轨迹并在此轨迹上寻找最值。而不等式的约束则需要分类讨论：一种情况是无约束条件下本身的最值就满足，这样有没有这个约束实际上没有区别，这个问题就只有等式约束。另一种情况是无约束条件下本身的最值不满足不等式约束，这样有约束问题的最值就会出现在满足全部或者一部分边界上，问题也可以转化为等式约束的极值优化。
以上这些是对产生极值的必要条件，即Karush-Kuhn-Tucker(KKT)条件的基本解释。等式约束可以使用Lagrange乘数法转化为一个无约束非线性优化问题，而无约束优化就可以采用上述提到的一系列方法计算。对于不等式约束仍需通过KKT条件简化后讨论是否可能作为等式约束加入优化过程中。对于上述问题，定义Lagrange函数为

其KKT条件可以表示为

其中第二三式可以认为是分别对Lagrange函数的和求导并令导数为0得到的，最后一行两式分别为对偶问题的可行性(Dual feasibility)和互补松弛性(Complementary slackness)。前者用于保证如果当前优化结果在边界上(即)，不存在往边界“内部”走还会出现比当前结果更小的点（即避免出现求解出的极值点在错误的边界上），后者代表了和中满足至少有一个为0，即至少满足无约束f(\vec{x})的极值点条件或者边界条件其中一个。
上面提到的KKT条件用于给出一般的非线性约束的优化问题的极值条件，这样至少可以在数值上验证其为最值并且指导相应优化算法的思路。下面列举一些常用的用于用于求解非线性约束的优化问题的算法，大部分主要针对的是等式约束的优化（不等式约束的优化可以通过有效集法转化为等式约束的优化）

投影梯度法

这个方法是用于求解线性等式或不等式约束的优化。其过程可以理解为在没有走出边界时采用梯度下降法优化，碰到边界或者落在在边界上是将迭代方向中垂直边界的分量去除，或者说将梯度投影到边界上，达到“贴着边界”走的优化。对于约束，带投影的下降方向表示为

二次规划

二次规划可以说是经典的二次型等式约束优化问题，其数学表示为

其中为对称矩阵。最直接的方法仍然是用Lagrange乘数法求导后解解线性方程组。对于上述问题其Lagrange函数表示为

分别对和求导并令其为0可得

通常将两个等式写成一个大矩阵的形式即

一般上述矩阵的规模都比较大，可以通过上述无约束优化方法中的如共轭梯度法等方式可以求解该方程。对于矩阵Q为正定矩阵的二次规划目标而言，如果存在满足上述条件的局部最优点那么它也是全局最优点，即二次规划中全局最优点只有一个。

有效集法(Active-Set)

有效集法，或者叫做积极集法，是通过判断不等式约束中哪些可以作为有效的等式约束进行优化，在不断迭代中找到有效的等式约束。具体的思路是：给定不等式约束中生效的约束作为初始有效集，先用求解等式约束的优化算法计算出极值点，然后验证该结果是否满足KKT条件。对于优化结果违反的不等式约束，将其作为等式约束加入有效集中，同时调整步长距离使得优化结果满足该约束；而对于计算出Lagrange乘数小于0对应的等式约束，可以认为该等式约束是错误的，将其从有效集中移除。调整有效集后再进行用Lagrange乘数法+无约束极值优化算法计算，重复直至算法收敛。上述过程用流程图表示为

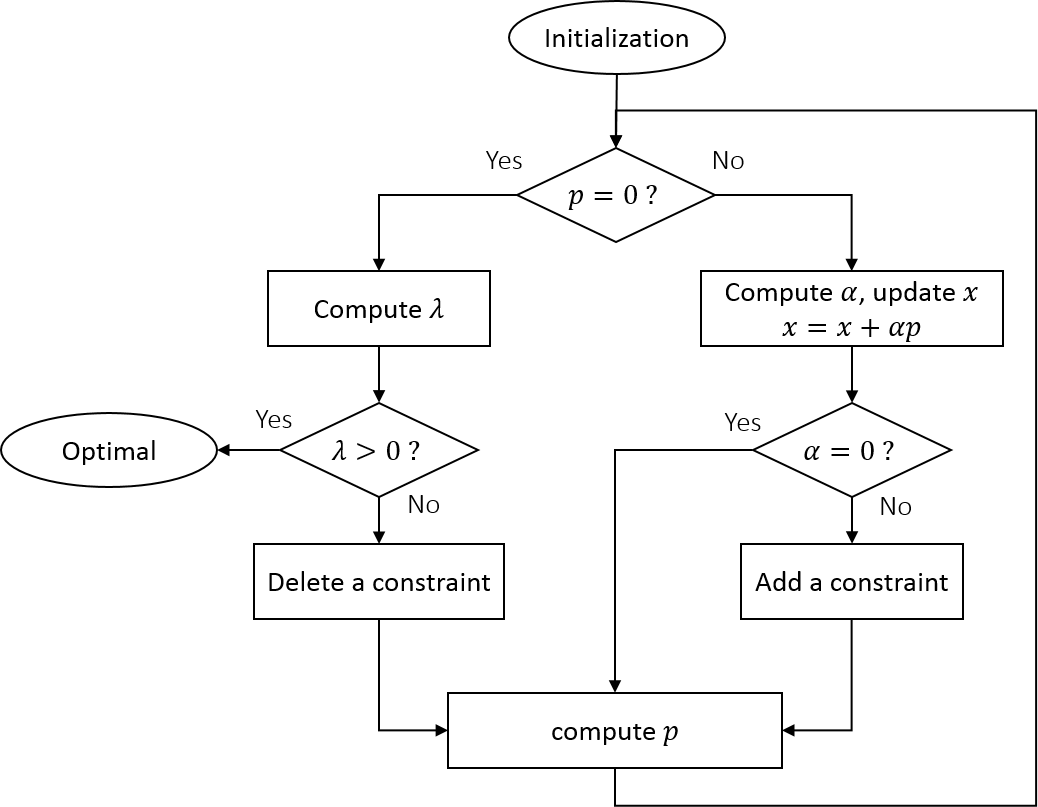
可见有效集法思路是将不等式约束转化为等式约束，再用等式约束的优化算法迭代求解。不过这个算法需要给定一个满足约束条件的初始解，求解初始解仍然绕不开求解不等式约束。

序列二次规划法(SQP)

对于上述非线性约束优化问题，如果只考虑等式约束，其Lagrange函数为

要求解极值点即为Lagrange函数导数为0的解，即求解方程。如果采用无约束优化算法里的牛顿法，其每一步的迭代式为，其中，展开迭代式表示为如下的矩阵形式

完全展开为等式之后可以发现第一行的等式中两边一项可以消去，再令，重新组成矩阵形式可以写为

如果参考二次规划(QC)问题的求解式，将每个矩阵表达式里的参数一一对应的，话我们发现实际上这个过程也是在求解一个如下的QC问题

将上述非线性的优化过程的每一步转化为一个QC子问题，这就是序列二次规划法(SQP)的核心。优化的目标函数并不是对原始函数的二阶近似，非要说的话也是对Lagrange函数的二阶近似。其迭代的思想虽然也是将整个非线性优化问题拆分为每一步优化的求解，但是其本质是牛顿法对Lagrange函数的迭代而不是“增加了约束的高斯牛顿法”。
SQP能够解决方向求解的问题，但在实践中都和其他算法组合使用，例如增加线搜索调整步长距离，使用BFGS计算Hession矩阵等

罚函数法

也被称作障碍函数法，将上述的等式和不等式约束的优化转化为无约束优化的一种方法。其思路是将违反约束作为惩罚加到目标函数上，让约束本身也作为最小化优化的目标之一。这样虽然求解上等效于无约束问题，但是软化了约束条件，同时由于罚函数的影响算法不一定能够精确地收敛至原函数的极值点上。

增广拉格朗日法

可以认为增广拉格朗日法罚函数法+拉格朗日法，它在原来Lagrange函数上增加了约束的二次项作为罚函数。若只考虑非线性约束优化问题中的等式约束，待优化的Lagrange函数写为

每次迭代除了逐渐增大惩罚参数以外还需要按照如下规则更新其余参数

数值积分方法

用于求解微分方程，或者说已知某点的微分求整条轨迹。数值计算总是离散的，因此积分方法也必须是基于离散值的积分。设，积分步长为，常用的积分方法主要有以下两种：

前向/后向欧拉积分

前向欧拉积分表示为

后向欧拉积分表示为

后向欧拉积分的需要通过迭代得到，即通过在同一个点上迭代的值。

龙格库塔法(Runge-Kutta,RK法)

参考