线性相机模型与标定方法

本文主要大部分是对 ZHANG Z. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.的解释

相机模型

相机模型主要用于描述相机的像素平面坐标系和世界三维坐标系之间的坐标映射关系。相机成像的模型可以用下图表示，以透镜的光心作为空间光线的三维坐标系，坐标系的Z轴垂直与成像平面即图像传感器的平面。

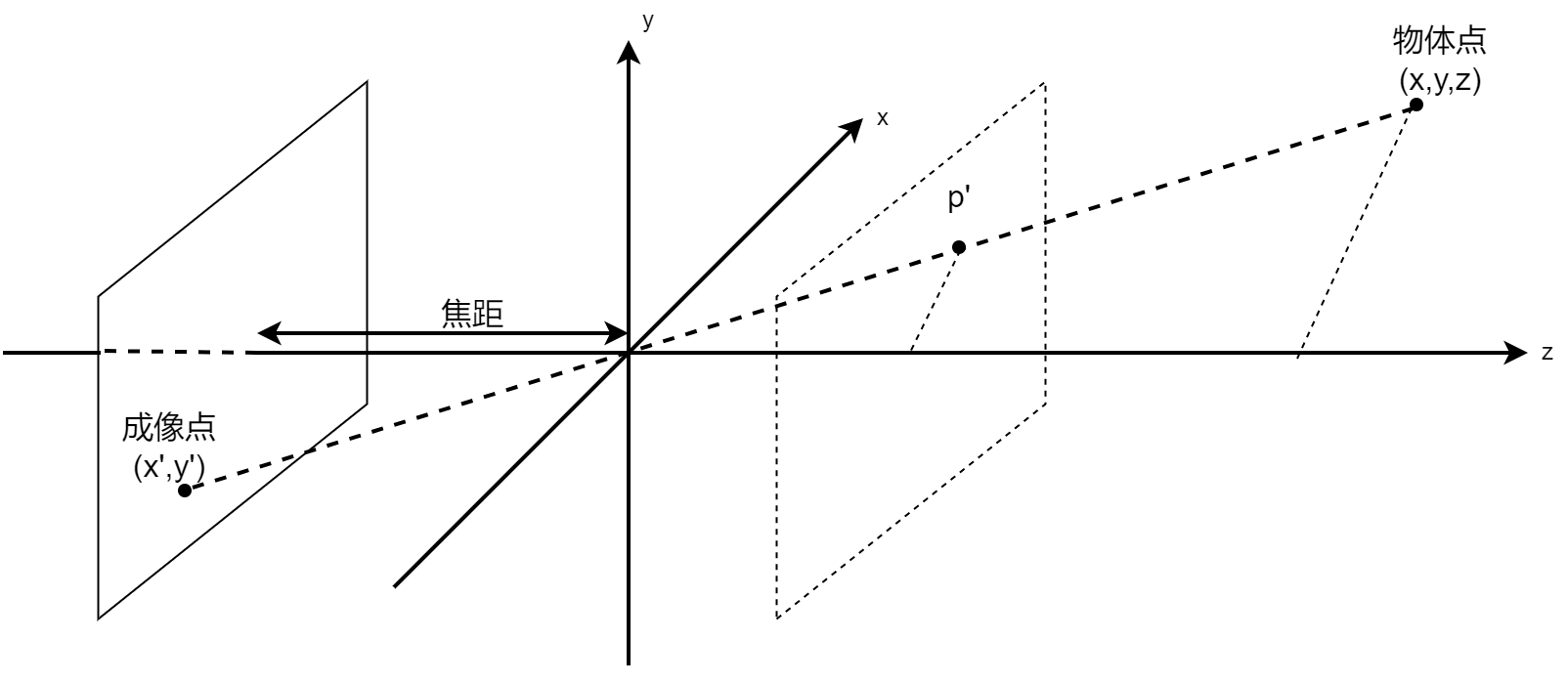
可以简单地认为相机成像平面坐标系下的二维点是由相机坐标系下的三维坐标点投影而来，即物体点的XY坐标与成像点的XY坐标之间分别存在相同的比例关系，满足如下等式，其中f为成像焦距

相机成像平面坐标到像素坐标系的转换可以由缩放+平移的线性变换表示，写成齐次形式为

世界三维坐标系下的点到相机三维坐标系可由旋转与平移变换得到

结合上述方程可以列出世界坐标系下的点到像素坐标系下的转换关系

一般可以将前两个矩阵写为一个3*4的矩阵，这里记为，其中前一个矩阵由于只与相机内部的光学结构相关，一般称矩阵内的四个参数为相机的内部参数，而后一个矩阵则是与相机相对于世界的外部条件相关，称其为外部参数。

标定算法

标定算法就是用于求解上面相机模型的参数，或者说通过一定的手段测量出相机的参数。可通过人工构造已知的特征点，将像素坐标系与三维空间坐标点对和对应起来，反过来通过求解线性方程组求解矩阵得到其变换关系，同时方程中的空间变换即摄影机的外部参数实际上是可变的，而内部参数相对稳定，我们希望标定过程能够将外部参数和内部参数分离，在求解后分离内部参数和外部参数。

单应性矩阵求解

针对特征点的构造，目前主要有棋盘格图样和圆形网格图样，这两种网格图样的获得相对简单，得到的特征点为三维世界坐标系下共面的网格点，并且网格的宽度已知。另外棋盘格除了特征较为明显容易定位外，通过计算棋盘格格子边缘对应直线的方程再求解交点可以实现亚像素级的顶点定位，在标定时能够尽可能精确地获取角点位置。
考虑到网格点在三维世界中共面，不妨以垂直该平面方向为Z轴定义世界坐标系，这样标定图样上所有世界坐标都可以表示为，设像素坐标的点对应的世界坐标，摄影机内参矩阵，三维旋转矩阵拆分为列向量形式即，代入上述相机模型可进一步化简

令，代入上述方程并展开可得

消去方程中的并将中的元素写为列向量的形式，可以得到如下的矩阵形式的线性齐次方程组，

同一图像上多个点可扩展上述方程左侧矩阵的行，通过联立若干个点求其最小二乘解即可获得矩阵中的所有参数。超定的齐次线性方程组的求解可以通过奇异值分解求解，取最小奇异值对应的特征向量即为方程的解。而由于对求解出的矩阵进行任意缩放后结果仍然满足上述方程，后面使用矩阵时都会带一个任意大小的缩放因子，确保解的齐次性仍然被保留。

内外参数分离

将求解出的矩阵取前两列作为一个新矩阵，根据性质满足方程

同时根据旋转向量的性质可以得到方程

令对称矩阵
代入上述方程可得

考虑到方程中的任意大小缩放因子，需要尽可能构造线性齐次方程，在列出的线性方程里消去。这里应选用作为待求解的方程。将待求解的方程中的矩阵的参数提取出来写成列向量的形式

求解该方程需要至少三张图片的相机单应性矩阵，求解得到五个参数后可一一对应计算出摄影机的四个内部参数和

求解出内参矩阵后，可将重新代入方程中，求解外参中的旋转矩阵和平移向量：

这里求解出的三个旋转向量再重组为旋转矩阵在归一化之后还需要重新正交化，确保求解出的矩阵满足旋转矩阵为正交矩阵的约束。按照原论文技术报告A Flexible New Technique for Camera Calibration 中的Approximating a 3 × 3 matrix by a Rotation Matrix中的解释，设重组后的矩阵为，则上述问题可以表示为求一个正交矩阵使其能够最佳近似原矩阵，即

该问题的解为，其中分别为矩阵的左奇异向量矩阵和右奇异矩阵，两者可以由奇异值分解获得。

标定误差验证

摄影机标定参数的准确程度可以用重投影误差表示，即在求解出所有参数后代入重新计算三维空间的点在像素坐标系下的位置，与原始图片中角点位置比较偏差大小，误差越小说明标定的精确程度越好。消去求解单应性矩阵方程中的，用内外参数组合求解出的，重新将世界坐标投影可得

对于上述重投影的点坐标，计算其与对应原坐标点之间的平方误差，取多个点对的均方根误差即为重投影均方根误差。该误差直接用于衡量标定算法的误差大小