入门强化学习

基本概念

强化学习是指机器通过与外部环境交互，学习最佳策略的过程。其中决策的主体被称为智能体(Agent)，它能够根据环境反馈的状态(State)，以及人为设计的描述输出动作好坏程度的奖励(Reward)做出相应的动作(Action)。这个过程的“最佳”体现在最终的目标是调整策略，使得总体奖励最大化。

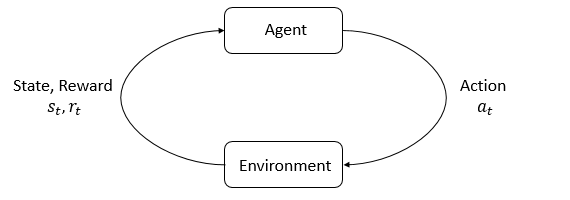
状态(State)：时刻的状态记为，所有可能的状态取值组成的空间称为状态空间(State Space)
动作(Action)：时刻的动作记为，所有可能的动作取值组成的空间称为动作空间(Action Space)。输出的动作可分为随机性动作和确定性动作。随机性动作由随机策略(Stochastic Policies)产生，输出的动作服从某个可参数化的关于状态的分布即。确定性的动作由确定性策略(Deterministic Policies)产生，输出的动作可以描述为一个参数化的关于状态的函数
奖励（回报,Reward）：时刻的奖励记为，可由一个关于状态（或者状态和动作）的函数获得。
轨迹：由各个时刻的组成的序列，记为
总体奖励：描述一条轨迹中的总奖励，一种描述为限无衰减的总回报(finite-horizon undiscounted return)

另一种无限有衰减的总回报(infinite-horizon discounted return)如下,其中\gamma为0到1之间的衰减系数。
价值函数(Value Function)，即从状态开始，按照策略输出动作的条件下奖励的数学期望
动作-价值函数(Action-Value Function)，即从状态开始并输出动作，随后按照策略输出动作的条件下奖励的数学期望

这里的状态(State)，动作(Action)，奖励(Reward)等变量是对真实系统中的变量的抽象。例如在倒立摆的控制问题中，状态是摆杆的角度、角速度、位移以及速度等参量，而动作则是输出到摆杆底端的水平方向驱动力的大小，奖励可能被人为设计为关于摆杆角度和保持直立的时间长短，摆杆的角度越小并且保持直立的时间越长奖励的值越大。

对于随机策略 $│$ ，它描述了策略在状态为输出动作为的概率，为该概率密度函数的参数，可代表策略本身。在该参数下出现轨迹的概率为
$│ │ │$
则强化学习中学习随机策略的优化目标可以认为是找到一个参数，使得随机过程中奖励的期望最大化
$│$

算法分类

策略梯度(Policy Gradients)

策略梯度方法的基本思想是根据奖励大小直接优化策略，简单而言就是能增加能获得奖励的输出，减小不获得奖励或奖励为负的策略输出。这里优化策略本身的方法也是基于梯度的方法（如梯度下降/上升法优化）。按照上面提到的随机策略的优化目标，待优化函数的梯度表示为
$│ │ │ │ │ │$
这里将梯度转换为对数形式，能将 $│$ 内的连乘项展开为求和，而连乘项中关于的函数只有一项 $│$ ，故 $│ │$ ，代入可得

$│ │ │$

上述策略梯度可以通过采样不同轨迹的统计值估计数学期望，求出梯度后在使用梯度方法对参数进行优化。
策略梯度方法实际上有许多改进与变种，其形式都是将上述梯度表达式中替换为其他可用于描述状态和动作与奖励直接关系的函数，常见的改进包括：

忽略当前动作以前的奖励，即替换为，避免轨迹中过去的奖励影响未来决策
增加基线，即替换为，其中为当前状态下随机策略的基准值。这样可以将某些奖励输出总是为正的情况变为有正有负，增加对策略的“惩罚”
动作-价值函数(Action-Value Function)，这个实际上结合了下面即将提到的基于价值评估的方法。
优势函数(Advantage Functions)，这个函数用于衡量该状态下做出某个动作相对于平均水平的好坏。

策略梯度方法的优势在于对策略的直接改进，基于真实轨迹的采样能够保证最终学习出的策略较为准确。但训练过程可能出现不稳定且方差较大，可通过Importance Sampling，以及TRPO和PPO等训练算法上的改进克服。

价值估计

价值估计方法通过拟合动作-价值函数并求在当前状态下使得该函数最大的动作作为输出，由于这类方法相当于是转换决策问题为学习函数，因此也被称作Q学习(Q-Learning)。根据贝尔曼方程(Bellman Equations)，总奖励函数为无限有衰减的总回报下，动作-价值函数以及价值函数满足：

贝尔曼方程的基本思想是当前的奖励，加上未来转换到的状态的带衰减的价值函数，即为当前的价值函数。贝尔曼方程告诉我们，如果能够准确拟合实际的的奖励函数的数学期望，那么就存在一个最优决策，该决策为选择当前状态下的使得最大化的动作。最优策略下的动作-价值函数可以表示为

基于上式通过统计采样的方法近似数学期望，可以得到的点对，再通过如查表法或神经网络等方法拟合得到用于决策的最优Q函数。实际输出的动作将基于该函数求其最大值。
价值估计方法在实际中除了对估计不准确外，由于使用该函数总是输出确定性的策略，算法对于环境缺乏探索，有时候较难收敛到最优策略中。针对该问题可采用ϵ贪心 (Epsilon Greedy) ，在一定概率下输出完全随机的动作作为探索。其他Q学习的改进包括Double DQN，Prioritized Experience Replay等。

Actor-Critic架构

基于Actor-Critic架构的方法结合了策略梯度和价值估计两种方法，既对价值函数进行拟合，又基于拟合的价值函数求策略梯度改进策略。Actor-Critic架构一般包括策略网络(Actor)和价值网络(Critic)两部分，前者用于输出动作，后者则是对当前价值函数进行估计。一个例子是Deep Deterministic Policy Gradient(DDPG)，它同时结合了策略梯度和深度Q网络(DQN)，用最小二乘拟合，同时增加Target Network降低价值估计网络的改变速度。算法的流程如下：

搬砖笔记