引入

这篇文章主要是记录看完(1)之后的笔记。在之前的提到的各种姿态估计的算法中，姿态的非线性是一个非常难处理的问题。试图用Kalman滤波器等线性方法估计状态只是一种近似的手段，IEKF也算是另外一种手段。
但上述这些方法都或多或少的有些奇怪，因为观测的状态本身总是不符合Kalman滤波器所要求的线性，而我们希望设定的姿态能满足可加和的性质。实际上在误差状态Kalman中就已经提到了一些关于流形(Manifolds)上的操作，比较专业一些的算法例如FAST-LIO设定的状态也是在流形上的。不过目前正是因为缺少这部分的基础知识，看不明白这些论文的方法，于是找了(1)(2)(3)几本书补一下。
文(2)(3)覆盖内容比较全面一些，而文(1)主要覆盖的是工程运用里面所用到的基础知识，比较适合速成，这里也主要是围绕(1)展开。

基本概念

• 流形(Manifold)：状态降维的抽象概念，表征高维数据中的低维结构，可以理解为为带约束的高维空间
• 李群(Lie Group)：一个光滑（可微分）的流形,且其元素满足如下性质：
  
• 切空间(Tangent space)：给定流形上随移动一点，其导数所构成的空间。可以理解为与流形相切的平面构成的空间，是流形在某一点处线性化的向量空间。流形上一点的切空间记作
• 李代数(Lie algebra)：流形在其幺元(Identity)处的切空间，可以理解为流形在其“原点”处线性化的向量空间。流形的李代数可记作

需要注意的是，流形的组合操作类似矩阵乘法，一般情况并不满足交换律。
实际上李群的概念并不是具体指代一种集合，而是说符合上述性质的一类抽象的集合，具体在现实中可能有很多种符合上述条件的集合。这些集合上很多操作都是非线性的，例如最常见的姿态表示的空间中旋转的组合都是采用乘法叠加的，这就为许多线性的信号处理的方法带来了麻烦。而在流形切空间上进行姿态的线性处理是一个非常合适的解决方法。虽然如扩展Kalman也可以直接对当前姿态状态求Jacobian近似线性化，但是流形切空间的优势在于由于流形上每一点总是相似的，其切空间也是相近的，这样其非线性程度远小于直接线性化。

问题提出

在之前ESKF或者EKF算法中采用四元数对姿态进行估计时，由于采用的是六轴传感器，Yaw轴的数据仅来源于Kalman的预测过程。在最后更新状态一步由于姿态融合的非线性，在加速度计数据通过线性融合进入四元数时会出现Yaw轴的额外偏移，使得最后积分结果偏离了角速度计积分出的Yaw轴结果。具体表现为当加速度计与角速度计数据较为不匹配时（例如受到冲击），Yaw会出现较大的偏移。

为了解决非线性带来的影响，除了消除线性更新中对于Yaw轴旋转的分量外，还需要进一步使用迭代Kalman滤波器(Iterated Extended Kalman Filter)的方法改进原有算法。

原理

在EKF算法更新环节中中，我们在工作点附近用线性过程替代实现线性的融合，而迭代Kalman滤波器的思路是不改变模型采用数值迭代的方法隐式地逼近状态估计值，即通过某种非线性的方法调整状态使得观测值和预测值两者与实际值之间的误差最小化。在数学上，令[1]

如果假设Z的分布符合，则在最大似然准则下可以取令Z的似然函数最大化时的状态值作为非线性的观测结果,也即最小化二次型

取其导数为0的点作为结果，带入后验方差的计算中可推导出与传统Kalman滤波器一样的方差更新公式。而对于状态值的更新则采用高斯-牛顿法求解，若令则

根据高斯-牛顿法的迭代过程，状态值的迭代式为

代入经过推导可以得到迭代式

另外如果结合之前的误差状态Kalman滤波器其迭代过程依然类似，最主要的区别仅在于与后面两项之和是在流形上相加[2]，当然也有为了进一步理想化非线性环节将一项也改写为流形上操作的[3]

原始算法

求某个数的平方根倒数是一个十分常见且高频的操作，比起直接调用数学库里的sqrt函数，一个显著快速的方法是这样的

1
2
3
4
5
6
7
8

float InvSqrt(float x){
	float xhalf = 0.5f*x;
	int i = *(int*)&x;
	i = 0x5f3759df - (i>>1);
	x = *(float*)&i;
	x = x*(1.5f-xhalf*x*x); 
	return x;
}

实际上这个算法可以说是为了性能完全牺牲了解释性，因为绝大多数人第一次看到它的时候可能完全摸不着头脑。本文除了详细解释算法的原理以外，还希望揣测算法编写者的动机，并在其他的数值算法性能的的优化上给出指导。

原理

引入

常见的许多滤波如Kalman滤波等，其中本质上最后一步都是将两个测量同一个信号的不同传感器的输出信号合成为一个信号，这种最为常见的“线性融合”的滤波在数学上简单地表示为

其中即为两个待融合的信号，这里姑且称为滤波器增益，直观上上看是对两个信号做线性插值(Lerp)。传统的频域分析认为而如果，即滤波器输出与上一个输出融合，这个滤波器就是一个IIR低通滤波器。而如果系统的动力学模型已知，则可以用Kalman滤波器计算出滤最优波器增益完成融合（具体原理在如何理解Kalman滤波已经提及）。而这里下面讨论的是只知道传感器测量值以及概率分布的情况，通过最大似然估计和最大后验估计这两种统计参数估计方法两种方法给出解释

原理

对于滤波器而言其核心的原理在于滤波的准则，Kalman滤波器的准则是选择使得后验误差最小化的滤波增益，经典滤波器的准则是保留特定频带的信号而消除其他频带上的信号。同样地只知道传感器测量值以及概率分布的情况估计真实信号的滤波器也会有其准则，采用最大似然估计方法的准则称为最大似然估计，采用最大后验估计的准则称为最大后验准则。这两种方法的下面只做了最简单的两个测量值融合的分析，实际上也很容易推导至更多测量值融合以及多维联合正态分布的情况。
这里需要说明的是，后面的分析基于下面几个假设：首先待估计的真实值为，从两个测量源得到的测量值分别为和，两个测量值均为独立并且存在高斯噪声与，即

最大似然估计

基础知识，其中在Joan Sola - Quaternion kinematics for the error-state Kalman filter中提到了ESKF的实现，这里将按照文中的思路尝试构建一个简单的六轴算法并给出对应的解释

原理与思路

基础思路

ESKF(Error-State Kalman Filter)也是一种Kalman滤波器，基础的内容也类似如何理解Kalman滤波滤波中提到的，本质上与EKF类似，但ESKF最为核心的部分是，状态设定为实际状态的变化值即，根据推导出系统Error-State状态方程观测出系统，最后将此误差值与系统状态融合得到更新后的状态。
对于线性系统而言ESKF实际上与普通的Kalman滤波并无太大区别，但是在非线性的系统中观测比观测非线性程度会进一步减弱，并且后面我们也可以发现，最后一步误差值“加上”系统状态的定义可以是广义的，旋转的误差可以采用乘法（四元数乘法等）融合进实际姿态里，使得观测过程更加精确

另外一点，文中算法定义的旋转的误差，是一个三维的矢量，也就是之前一文中提到的so(3)的向量空间，比起其他的采用四元数直接相加的融合算法少了约束，因此这个整个滤波过程看上去更加像是拥有符合Kalman滤波器所需要的线性

数学模型

状态变量、输入/输出

状态空间方程是描述线性系统相互制约的关系的一种方式，其中主要有以下的三个变量

• 外部环境对系统的作用也即外部施加的激励，为系统的输入，一般用多维列向量表示
• 描述系统内部所处的行为或者运动信息的变量，为系统的状态量，一般用多维列向量表示
• 能够从外部直接测量到的系统对外部环境的作用，为系统的输出一般用多维列向量表示

三个变量中一般可获知的变量只有系统的输入和输出，系统内部的状态量一般不能直接测量得到。同一个系统可以存在不同状态量表示的形式，其变量不一定存在物理意义。但有效状态量的数量是可以确定的，由n阶微分方程所确定的系统内部状态量向量的维数也为n，即系统状态量最大线性无关元素的个数为n

这篇文章只是提出一个运营上的模式，只是我个人经验总结而来的，仅供参考。从技术角度看向研发的管理，无非是要使制定一个计划保证研发的必要性和可行性，过程能够被量化，并确保最终结果合乎期望。下面是一个我认为研发最开始的时候应该要清楚的几个关键点，这些也可以作为一个立项模板来填写

问题定义

至少能够给出需要解决的问题的定义并说明必要性，这里一般是研发的，时间线会比较长的问题，例如说上个赛季从比赛结果来看我们出了什么问题。一般也不能是太广的问题例如所有机器人的稳定性，而是稍微的具体问题例如我们在与某个学校的比赛中因为机动性不足而处于劣势，因此需要提升步兵机器人的机动性，而后我们可以思考如何衡量机动性这一指标并给出解决方案。又或者说我们发现我们的阵容不足以击败一些强队，需要一台平衡步兵等。当然这里说明必要性也可以给出量化的指标，增强说服力。

需求分析

实际测试

RoboMaster比赛中，弹道解算是指根据视觉系统识别到的击打位置，计算云台应指向的角度的算法，这也是自动瞄准算法的最后一环。实际上相当于一个根据预测弹道轨迹反求瞄准角度的算法

理论计算

在视觉方案上计算的方案(1)(2)早已有人实现并被广泛使用，然而这两个算法均基于将弯曲的弹道补偿为直线，并且采用简单的迭代求数值解的思路编写。我认为这两个思路均比较奇怪，因为实际上在不考虑空气阻力的抛物体模型下非常容易求出解析解，而即使考虑了空气阻力计算出的结果也应与无空气阻力相近，另外迭代的危险之处在于可能存在计算失败的情况（数值上不收敛，或者方程本身是无解的）。针对这些问题，下面本文试图通过解析方法分别分析在无空气阻力模型和有空气阻力模型下求解发射角度的过程，以及一些边界情况的判定条件。

无空气阻力模型

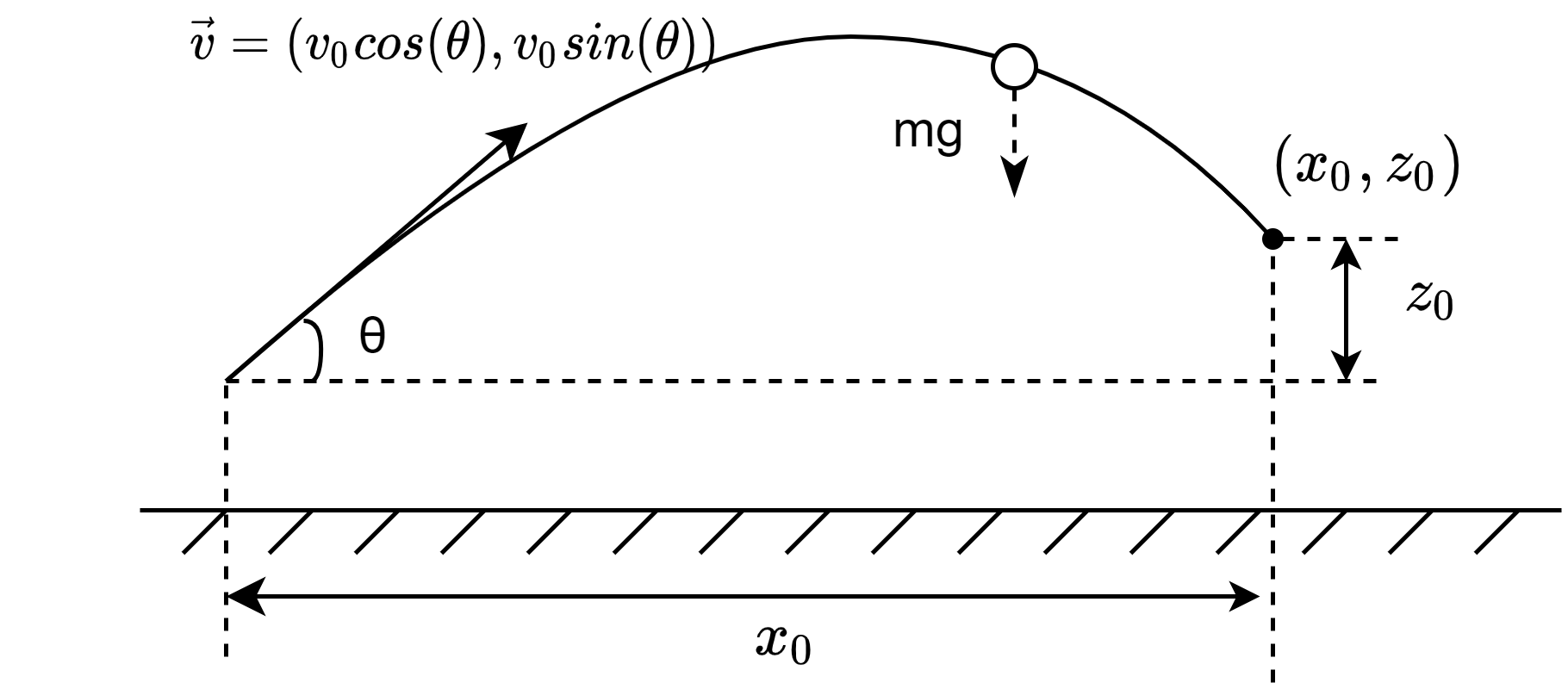
如上图，只考虑弹丸在竖直平面（沿重力加速方向）运动的情况，假设目标（图中实心圆）距离发射点x0，竖直高度差为z0。以初始速度v将弹丸发射，发射出去的弹丸（图中空心圆）仅受重力影响。可列出如下方程

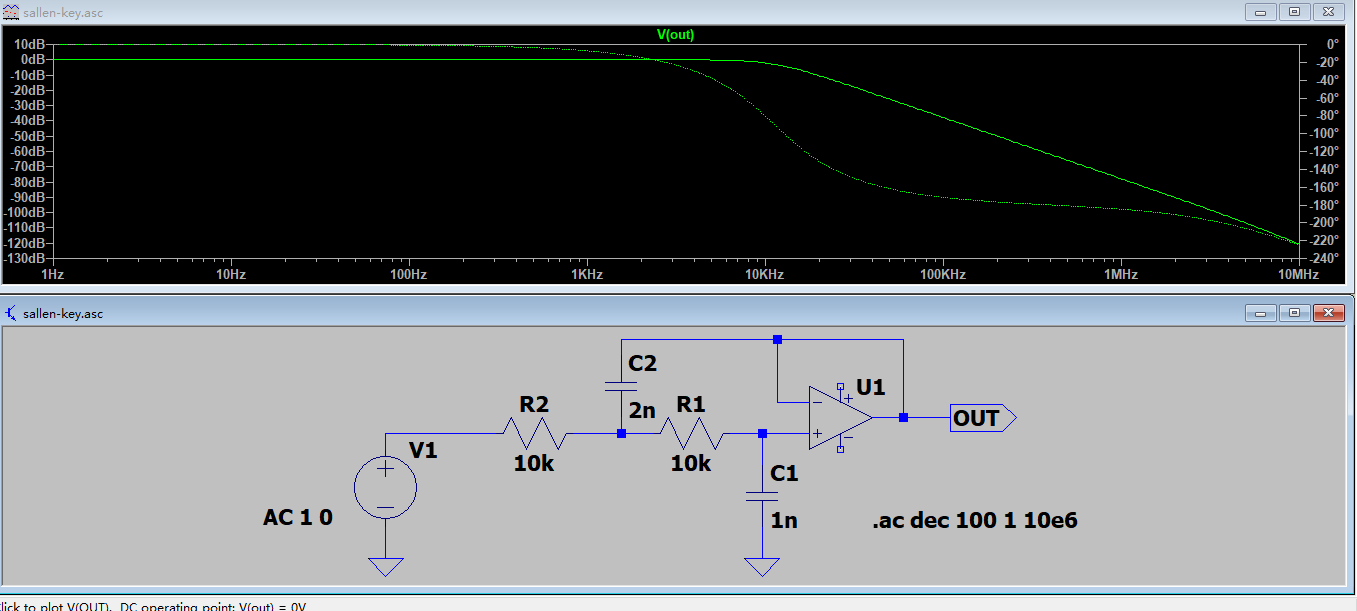
所谓电路仿真，是指对设计出的电路的实际功能进行模拟。为了最大程度确保电路在实际工程中符合预期，在如今EDA如此发达的时代几乎几乎每个电路设计的流程里面都会用仿真，采用计算机仿真也成了硬件设计的必备技能之一。下面在这里简单介绍一些常用的仿真软件以及使用。由于在RM里硬件的考察主要为超级电容模块的制作，也就是功率硬件的方向，因此这里的仿真将更加侧重于功率电源方向。

SPICE原理仿真

SPICE(Simulation Program with Integrated Circuit Emphasis)为一个早期开源的电路原理仿真的软件，后续衍生出不少的版本。这些版本也由一些半导体厂/电子厂直接开发而来，例如Candence的PSpice，Ti公司版本的PSpice以及用于模拟电路仿真的Tina-Ti，目前我们课堂上用过的NI的Multisim，ADI公司版本的LTSpice，还有开源版本的ngspice（Kicad内置的仿真软件即为这个）

就我个人而言，比较常用的是LTSpice和Tina-Ti，这两个软件可以免费使用，并且LTSpice仿真的速度极快，一般小型的电路10ms的仿真基本上秒出结果。两者均可以进行稳态/瞬态仿真，幅频相频响应仿真，对于目前能接触到的绝大部分电路均可使用。同时SPICE仿真也可以导入厂商给出的IC模型，可参考LTspice 入门教程3 导入仿真模型，对于官方库内不存在的元件也能手动添加参与仿真

基础知识回顾，在这篇文章中提到了Heikki Hyyti, Arto Visala的论文A DCM Based Attitude Estimation Algorithm for Low-Cost MEMS IMUs所采用的算法。这篇文章将详细补充评析论文中原理与实现的各个细节.

原理

基础知识

在如何理解Kalman滤波中列举过典型的Kalman滤波的过程如下

预测过程