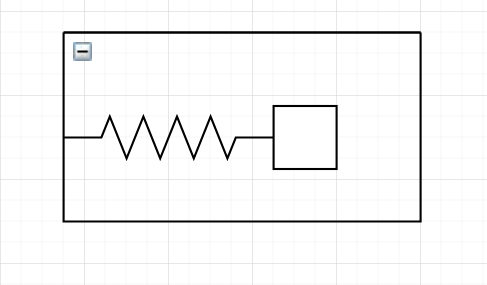
PID基础
所谓PID是指比例(Proportion)、积分(Integral)、微分(Differential)三者组合的控制算法,他以预期控制达到的目标值与当前系统反馈值作为误差执行以上操作,即
或者写成离散形式,其中Ki与Kd 省略了积分和微分的周期T
其控制的大致过程可以按照如下方式理解:首先比例项能够使误差趋近于0,因为大于或小于目标值都会使得比例项给出一个输出调节系统。
之前在Memfault的博客上发现了一个很有意思的日志库Trice。它专为嵌入式设备设计输出日志体积小型且可以以极高速率输出日志。作者号称在不输出时间戳的情况下可以用四条指令即可完成打日志,原因在于它并不会直接输出某个字符串,而是给每个字符串预先分配一个独一无二的ID(当然这部分在代码生成的时候完成),在打日志时候真正输出的是ID,通过上位机的程序解析输出。同样也具有printf格式化字符串的功能。
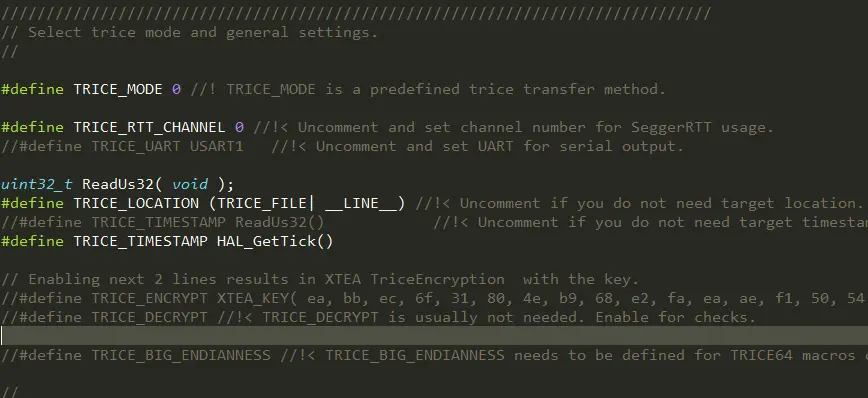
作为测试在这里也稍微提一下串口的使用方式。在代码配置中作者给出了阻塞非阻塞输出,前者直接等待输出完成,后者则是将输出内容写在缓冲区内等待空闲时输出,而硬件上目前只有串口和RTT,具体可以在triceConfig.h中修改TRICE_MODE完成
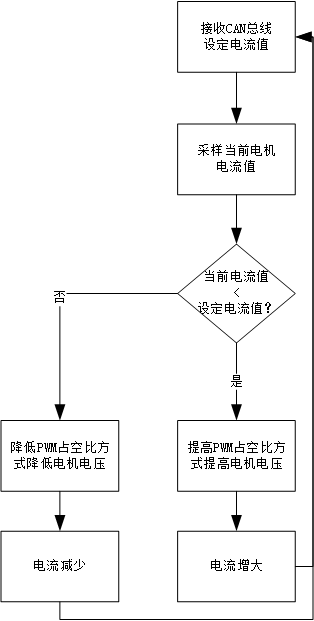
在RoboMaster系列电机中,GM6020电机是通过CAN总线控制电机电压,M3508电机是通过CAN总线控制电机电流。故而当M3508电机接收到CAN总线发送的电流设定值后,会通过一套控制算法来保证电机电流恒定
M3508电机比GM020电机相比,多了电流比较部分,通过一套控制算法调节电机电压,保证电机电流恒定,由于电机扭矩与电机电流成正比,进而控制电机扭矩恒定。M3508在空载启动时,电机负载扭矩较小,即使设定较小的电流控制值,电机也会很快加速,直至电机电压到达最大电压,之后电流逐渐减少,直至最大转速。
控制电流范围为-30000~30000,超过该范围仍然会输出,但是到达转速上限后电流会被抑制。已知转速存在限制(默认60rpm),需要外接串口修改上限,上限最高为300rpm。超过对应上限输出电压将被抑制
发送频率最高至1kHz,更高的频率无法响应;
发送频率最低约为5Hz,即为在间隔大于约200ms时间内CAN不发送数据时,电调将默认把输出电流置零
输出电压 = 反电动势 + 转矩电压(电机反馈数据) = 转速/转速常数(Ke)+ 转矩电压
控制流程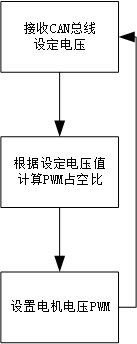
电机原始角度输出带低通滤波器,其闭环控制传递函数-3dB点<10Hz(1kHz控制频率测试,只有比例环节,kp=10,系统总是稳定)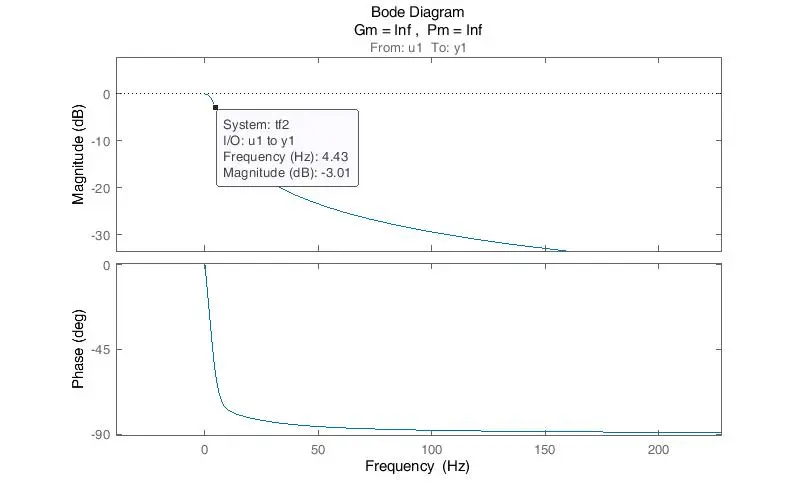
电机原始转速输出无滤波,其闭环控制传递函数-3dB点约为75Hz(1kHz控制频率测试,只有比例环节,kp=30,穿越频率位于79Hz,幅频尖峰出现在约50Hz附近)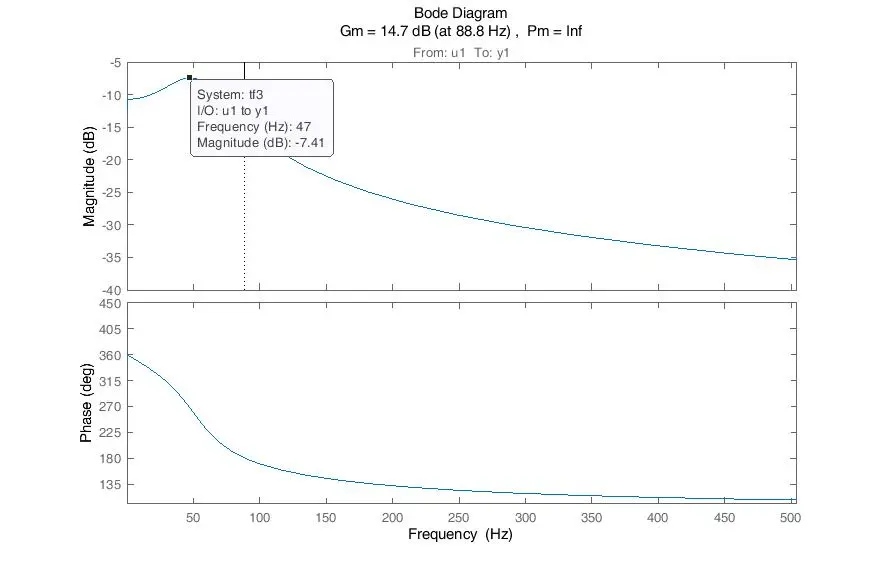
电机电流环带宽在80Hz~100Hz之间(1kHz控制频率堵转测试,直接输出扫频电压设定值)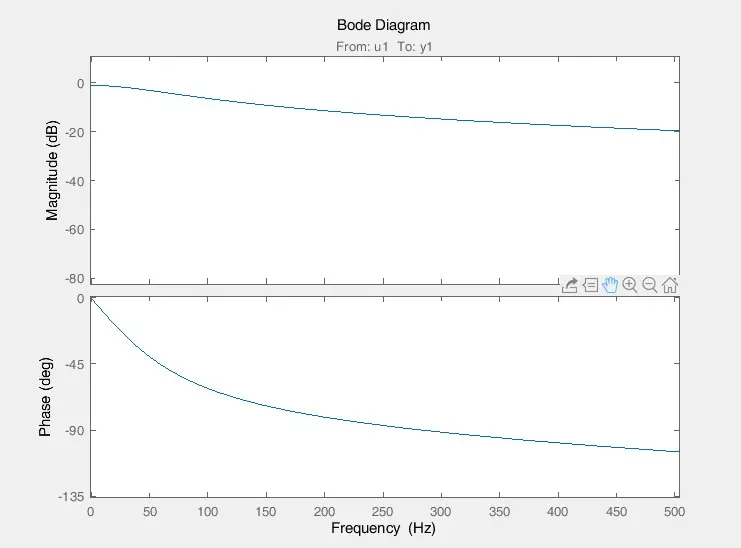
通常角速度计的真实值可以简单地用以下式子表示
其中A代表了尺度因子误差以及跨轴影响,b代表角速度计的偏置,其中包含了固有零偏,每次上电带来的随机偏差,温度变化带来的零偏。N则代表角速度计采样值的噪声,可以将量化噪声,角度随机游走以及零偏不稳定等归入此项。后两个也是角速度计两个重要的性能指标。
通常情况下,在短时间的积分中影响计算出的角度的误差主要是偏置项,通常校准偏置有以下几种手段:
CORDIC(Coordinate Rotation Digital Computer)算法即坐标旋转数字计算,这个算法的神奇之处在于它可以借助加减法、移位以及查表完成常见的超越函数(三角函数,反三角函数,对数,开根号)的计算,而不用多项式展开或者浮点数的计算。
所谓坐标旋转可以理解为在例如直角坐标系下的通过旋转矢量完成求解,对于一个坐标(x,y) 可以由初始(x_0,y_0)通过旋转矩阵得来,即
以计算正弦和余弦为例,CORDIC算法是预先求出(1/2)^n的反正切制成一个表,当我们输入一个预期角度时,通过比较当前角度与预期角度的大小确定旋转的方向d(仅代表正负符号),然后计算
巧妙的一点是,(1/2)^n恰好可以用右移来完成,而cos(theta)则是作为一个缩放因子,在迭代次数固定时也可以累乘预先计算。
这个迭代每次都会查表并且把反正切对应的角度加入当前角度,直到指定的迭代次数。这时计算出的角度应该非常接近对应角度,而旋转出的x_(n+1),y_(n+1)则应该是分别对应经过缩放的正弦值和余弦值。
本以为国电选信号失真度测量装置(A 题)题(几乎和之前的校赛一模一样),难度就会大大下降,结果还是要和所有人一起从零开始熟悉MSP430系列,最后测评还出问题了,寄。
题目这里就不贴了,在校赛的基础上改为直接测量外部信号发生器产生的波形,限定使用MSP430系列,电压范围30mV ~ 600mV,基频固定1kHz,失真度误差在5%以内,发挥部分大概就是手机显示波形和测量结果,更宽的电压范围和更小的误差范围以及1kHz ~100kHz基频范围。
看到这里我大概知道只要把输入信号稍微放大,ADC采样后用FFT分析即可,至于变基频无非就是写算法找频谱峰值,宽电压范围有点麻烦,需要做变增益控制,不过这个可以放着,而手机显示外接个蓝牙串口也可以完成。
所谓IMU(Inertial Measurement Unit)是指惯性测量单元,利用惯性的变化测量物体加速运动和旋转。其中目前主流的惯性测量器件是MEMS(微机电)传感器,它将用于机械结构缩小至纳米尺度,可测量机器人加速度与旋转角速度。后面讨论的内容应该可以归为捷联式惯导系统(Strapdown Inertial Navigation System),即测量单元直接安装于被测物体上,与平台式惯导系统区别开来。
需要注意的是,IMU或者说六轴(6Dof)传感器讨论的是三轴加速度计和三轴角速度计(俗称陀螺仪),与AHRS(航姿参考系)或者说9轴(9Dof)传感器是有区别的,后者增加了磁力计,以地磁场作为参考。但是在地面机器人运动并且夹杂大量电机磁干扰的情况下,引入微弱的地磁作为绝对航向并不是一个好主意。